2023年江蘇省連云港市東海縣中考數學一模試卷
發布:2024/4/20 14:35:0
一、選擇題(本大題共有8小題,每小題3分,共24分.在每小題給出的四個選項中,只有一項是符合題目要求的,請將正確選項前的字母代號填涂在答題卡相應位置上)
-
1.-
的相反數是( )35A.- 35B. 35C. 53D.- 53組卷:762引用:26難度:0.9 -
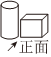 2.如圖,水平的講臺上放置的圓柱形筆筒和長方體形粉筆盒,其俯視圖是( )
2.如圖,水平的講臺上放置的圓柱形筆筒和長方體形粉筆盒,其俯視圖是( )A. 
B. 
C. 
D.  組卷:125引用:6難度:0.7
組卷:125引用:6難度:0.7 -
3.下列運算中正確的是( )
A.x2y+2yx2=3x2y B.3y2+4y3=7y5 C.a+a=a2 D.2x-x=2 組卷:941引用:14難度:0.8 -
4.將不等式x-3>0的解集表示在數軸上,正確的是( )
A. 
B. 
C. 
D.  組卷:82引用:3難度:0.7
組卷:82引用:3難度:0.7 -
5.某班有40人,一次體能測試后,老師對測試成績進行了統計.由于小亮沒有參加本次集體測試,因此計算其他39人的平均分為90分,方差s2=41.后來小亮進行了補測,成績為90分,關于該班40人的測試成績,下列說法正確的是( )
A.平均分不變,方差變大 B.平均分不變,方差變小 C.平均分和方差都不變 D.平均分和方差都改變 組卷:4765引用:51難度:0.5 -
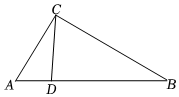 6.如圖,在△ABC中,D是AB邊上的點,∠B=∠ACD,,則△ADC與△ABC的面積比是( )AC:AB=1:2
6.如圖,在△ABC中,D是AB邊上的點,∠B=∠ACD,,則△ADC與△ABC的面積比是( )AC:AB=1:2A. 1:2B.1:2 C.1:3 D.1:4 組卷:209引用:6難度:0.7 -
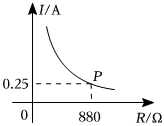 7.某個亮度可調節的臺燈,其燈光亮度的改變,可以通過調節總電阻控制電流的變化來實現.如圖所示的是該臺燈的電流I(A)與電阻R(Ω)的關系圖象,該圖象經過點P(880,0.25).根據圖象可知,下列說法正確的是( )
7.某個亮度可調節的臺燈,其燈光亮度的改變,可以通過調節總電阻控制電流的變化來實現.如圖所示的是該臺燈的電流I(A)與電阻R(Ω)的關系圖象,該圖象經過點P(880,0.25).根據圖象可知,下列說法正確的是( )A.當I<0.25時,R<880 B.I與R的函數關系式是 I=200R(R>0)C.當R>1000時,I>0.22 D.當880<R<1000時,I的取值范圍是0.22<I<0.25 組卷:1117引用:19難度:0.5 -
8.如圖1和圖2,已知點P是⊙O上一點,用直尺和圓規過點P作一條直線,使它與⊙O相切于點P.以下是甲、乙兩人的作法:
甲:如圖1,連接OP,以點P為圓心,OP長為半徑畫弧交⊙O于點A,連接并延長OA,再在OA上截取AB=OP,直線PB即為所求;
乙:如圖2,作直徑PA,在⊙O上取一點B(異于點P,A),連接AB和BP,過點P作∠BPC=∠A,則直線PC即為所求.
對于甲、乙兩人的作法,下列判斷正確的是( )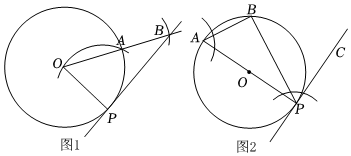
A.甲、乙兩人的作法都正確 B.甲、乙兩人的作法都錯誤 C.甲的作法正確,乙的作法錯誤 D.甲的作法錯誤,乙的作法正確 組卷:625引用:14難度:0.5
二、填空題(本大題共8小題,每題3分,共24分.不需要寫出解答過程,請把答案直接填寫在答題卡相應位置上)
-
9.要使式子
有意義,則x的取值范圍是 .2-x組卷:444引用:91難度:0.7
三、解答題(本題共11小題,共102分.解答時寫出必要的文字說明、證明過程或演算步驟)
-
26.如圖,已知拋物線
經過點A(-6,0),B(2,0),與y軸交于點C.y=12x2+bx+c ?
?
(1)求拋物線的解析式;
(2)若點P為該拋物線上一動點.
①當點P在直線AC下方時,過點P作PE∥x軸,交直線AC于點E,作PF∥y軸.交直線AC于點F,求EF的最大值;
②若∠PCB=3∠OCB,求點P的橫坐標.組卷:614引用:3難度:0.4 -
27.問題提出:(1)“弦圖”是中國古代數學成就的一個重要標志.小明用邊長為5的正方形ABCD制作了一個“弦圖”:如圖①,在正方形ABCD內取一點E,使得∠BEC=90°,作DF⊥CE,AG⊥DF,垂足分別為F、G,延長BE交AG于點H.若EH=1,求BE的長;

變式應用:(2)如圖②,分別以正方形ABCD的邊長AB和CD為斜邊向內作Rt△ABE和Rt△CDF,連接EF,若已知∠AEB=∠CFD=90°,AE=CF,Rt△ABE的面積為8,EF=3,則正方形ABCD的面積為 .2
拓展應用:(3)如圖③,公園中有一塊四邊形空地ABCD,AB=BC=60米,CD=120米,AD=60米,∠ABC=90°,空地中有一段半徑為60米的弧形道路(即2),現準備在?AC上找一點P將弧形道路改造為三條直路(即PA、PB、PC),并要求∠BPC=90°,三條直路將空地分割為△ABP、△BCP和四邊形APCD三個區域,用來種植不同的花草.?AC
①則∠APC的度數為 ;
②求四邊形APCD的面積. 組卷:447引用:4難度:0.1
組卷:447引用:4難度:0.1


