2023年湖北省黃石市大冶市東岳中學中考數學一模試卷

一、選擇題

• 1．下列說法正確的是（　　）

  A．倒數等于它本身的數只有1

  B．平方等于它本身的數只有1

  C．立方等于它本身的數只有1

  D．正數的絕對值是它本身
  組卷：1298引用：42難度：0.9

  解析

• 2．下列圖形是軸對稱圖形的是（　　）

  A．等腰三角形

  B．直角三角形

  C．三角形

  D．四邊形
  組卷：71引用：3難度：0.9

  解析

• 3．用5個完全相同的小正方體組合成如圖所示的立體圖形，它的俯視圖為（　　）

  A．

  B．

  C．

  D．
  組卷：48引用：5難度：0.9

  解析

• 4．下列計算正確的是（　　）

  A．6a+2b=8ab	B．a4?a2=a8
  C．4a3b÷ab=4a2	D．（ab2）4=a4b6
  組卷：279引用：5難度：0.7

  解析

• 5．函數y=

  2

  x

  +

  2

  自變量x的取值范圍是（　　）

  A．x≠2

  B．x≠-2

  C．x＞-2

  D．x＞2
  組卷：852引用：7難度：0.8

  解析

• 6．某學習小組的6名同學在第一次數學測試中的成績分別是94分、98分、90分、94分、80分、90分，則下列結論正確的是（　　）

  A．中位數是90分	B．眾數是94分
  C．平均數是91分	D．極差是20
  組卷：37引用：2難度：0.9

  解析

• 7．如圖，在平面直角坐標系中，A（1，0），B（-2，4），AB繞點A順時針旋轉90°得到AC，則點C的坐標是（　　）

  A．（4，3）

  B．（4，4）

  C．（5，3）

  D．（5，4）
  組卷：1413引用：4難度：0.5

  解析

• 8．如圖，△ABC內接于⊙O，∠A=60°，

  BC

  =

  8

  3

  ，D是AC的中點，則BD的長度的最大值是（　　）

  A． 8 3

  B． 4 13

  C． 4 7 + 4

  D．8
  組卷：1100引用：2難度：0.3

  解析

三、解答題

• 24．在平面直角坐標系xOy中，點P（x₀，y₀）到直線Ax+By+C=0（A²+B²≠0）的距離公式為：d=

  |

  A

  x

  0

  +

  B

  y

  0

  +

  C

  |

  A

  2

  +

  B

  2

  ，例如，求點P（1，3）到直線4x+3y-3=0的距離．
  解：由直線4x+3y-3=0知：A=4，B=3，C=-3，
  所以P（1，3）到直線4x+3y-3=0的距離為：d=

  |

  4

  ×

  1

  +

  3

  ×

  3

  -

  3

  |

  4

  2

  +

  3

  2

  =2．
  根據以上材料，解決下列問題：
  （1）求點P₁（1，-1）到直線3x-4y-6=0的距離；
  （2）已知：⊙C是以點C（2，1）為圓心，1為半徑的圓，⊙C與直線y=-

  3

  4

  x+2b相切，求實數b的值；
  （3）如圖，設點P為問題2中⊙C上的任意一點，點A，B為直線3x+4y+5=0上的兩點，且AB=4，請求出△ABP面積的最大值和最小值．
  組卷：142引用：4難度：0.4

  解析

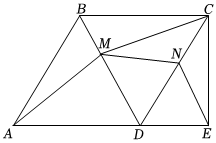• 25．如圖，△ADB與△BCD均為等邊三角形，延長AD到E，使∠AEC=90°，AD=5，動點M從點B出發，沿BD方向運動，移動速度為1個單位/秒，同時，點N由點D向點C運動，移動速度為2個單位/秒，其中一個到終點，都停止運動，連接AM，CM，MN，NE，設運動時間為t（0≤t≤2.5）．
  （1）t為何值時，MN∥BC；
  （2）連接BN，t為何值時，B、N、E三點共線；
  （3）設四邊形AMNE的面積為S，求S與t的函數關系式；
  （4）是否存在某一時刻t,使N在∠CMD的角平分線上，若存在，求出t近似值；若不存在，說明理由．
  組卷：26引用：1難度：0.2

  解析