2022-2023學年吉林省長春外國語學校八年級（上）期末數學試卷

一、選擇題

• 1．下列運算正確的是（　　）

  A．2a?3b=5ab

  B．a2?a3=a5

  C．（2a）3=6a3

  D．a6÷a2=a3
  組卷：319引用：16難度：0.9

  解析

• 2．要使二次根式

  5

  x

  -

  2

  在實數范圍內有意義，則x的取值范圍是（　　）

  A． x = 2 5

  B． x ≠ 2 5

  C．x≥ 2 5

  D．x≤ 2 5
  組卷：962引用：5難度：0.8

  解析

• 3．估計

  1

  +

  7

  的值在（　　）

  A．1到2之間

  B．2到3之間

  C．3到4之間

  D．4到5之間
  組卷：85引用：1難度：0.7

  解析

• 4．下列二次根式中，與

  3

  是同類二次根式的是（　　）

  A．6

  B． 9

  C． 12

  D． 18
  組卷：620引用：53難度：0.7

  解析

• 5．在下列四組數中，不是勾股數的一組數是（　　）

  A．15，8，17

  B．6，8，10

  C．5，12，13

  D．3，5，7
  組卷：193引用：4難度：0.6

  解析

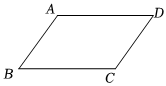• 6．如圖，?ABCD的周長為30，AD：AB=3：2，那么BC的長度是（　　）

  A．9

  B．12

  C．15

  D．18
  組卷：937引用：5難度：0.6

  解析

• 7．四邊形ABCD的對角線互相平分，要使它變為矩形，需要添加的條件是（　　）

  A．AB=CD

  B．AD=BC

  C．AB=BC

  D．AC=BD
  組卷：938引用：46難度：0.7

  解析

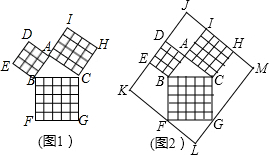• 8．勾股定理在平面幾何中有著不可替代的重要地位，在我國古算書《周髀算經》中就有“若勾三，股四，則弦五”的記載．如圖1是由邊長均為1的小正方形和Rt△ABC構成的，可以用其面積關系驗證勾股定理．將圖1按圖2所示“嵌入”長方形LMJK，則該長方形的面積為（　　）

  A．120

  B．110

  C．100

  D．90
  組卷：1951引用：7難度：0.5

  解析

三、解答題

• 25．[教材呈現]下面是華師版八年級下冊數學教材第104頁的部分內容．
  

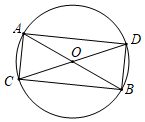  1．如圖，AB、CD是⊙O的兩條直徑，四邊形ACBD是矩形嗎？證明你的結論．

  [問題解決]如圖①，AB、CD是⊙O的兩條直徑．
  求證：四邊形ACBD是矩形．
  [發現結論]矩形的四個頂點都在以該矩形對角線的交點為圓心，對角線的長為直徑的圓上．
  [結論應用]如圖②，已知線段AB=2，以線段AB為對角線構成矩形ACBD，矩形ACBD面積的最大值為

  ．
  [拓展延伸]如圖③，在矩形ABCD中，AB=2，∠ADB=30°，點E、F分別為邊AD、BC的中點，以線段EF為對角線構造矩形EGFH，矩形EGFH的邊與矩形ABCD的對角線BD交于M、N兩點，當MN的長最長時，矩形EGFH的面積為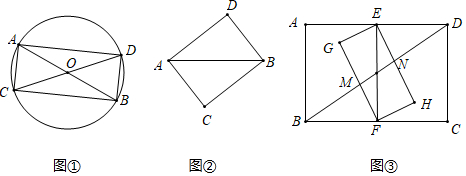

  ．
  
  組卷：253引用：4難度：0.2

  解析

• 26．如圖，在正方形ABCD中，AB=1，延長BC至M，使BM=6．以BD、BM為鄰邊作?DBMN．動點P從點D出發，以每秒2個單位的速度沿DN向終點N運動，過點P作PQ⊥BM交BM或BM的延長線于點Q，以PQ為邊向右作正方形PQRS．設正方形PQRS與?DBMN的重疊部分的面積為y,點P運動的時間為t（t＞0，單位：秒）．
  
  （1）用含t的代數式表示線段PN為

  ；
  （2）當點S與點N重合時，求t的值；
  （3）當正方形PQRS與?DBMN的重疊部分不是正方形時，用含t的代數式表示y；
  （4）當△DQS或△PRN是銳角三角形時，直接寫出t的取值范圍．
  組卷：79引用：1難度：0.3

  解析