2022-2023學年北京四十四中八年級（下）期中數學試卷

一、選擇題（每題2分，共20分）

• 1．下列二次根式中，屬于最簡二次根式的是（　　）

  A． 1 2

  B． 8

  C． 5

  D． 27
  組卷：139引用：1難度：0.7

  解析

• 2．下列四組線段中，可以構成直角三角形的是（　　）

  A．1，1，1

  B．2，3，4

  C．1，2，3

  D．5，12，13
  組卷：598引用：19難度：0.6

  解析

• 3．若式子

  x

  -

  1

  在實數范圍內有意義，則x的取值范圍是（　　）

  A．x≠1

  B．x＞1

  C．x≥1

  D．x≤1
  組卷：638引用：26難度：0.9

  解析

• 4．在?ABCD中、如果∠A=65°、那么∠C的度數是（　　）

  A．115°

  B．65°

  C．25°

  D．35°
  組卷：697引用：7難度：0.6

  解析

• 5．直角三角形的兩條直角邊的長分別為5和12，則斜邊上的高為（　　）

  A． 60 13

  B． 13 2

  C．6

  D．13
  組卷：512引用：5難度：0.6

  解析

• 6．如圖，在?ABCD中，AE平分∠BAD，交CD邊于E，AD=3，EC=2，則AB的長為（　　）

  A．1

  B．2

  C．3

  D．5
  組卷：592引用：18難度：0.7

  解析

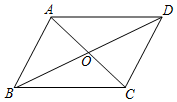• 7．如圖所示，在平行四邊形ABCD中，對角線AC、BD相交于點O，下列條件不能判定平行四邊形ABCD為矩形的是（　　）

  A．∠ABC=90°

  B．AC=BD

  C．AD=AB

  D．∠BAD=∠ADC
  組卷：3578引用：17難度：0.5

  解析

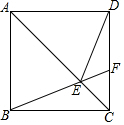• 8．如圖，在正方形ABCD中，點F為CD上一點，BF與AC交于點E．若∠CBF=20°，則∠DEF的度數是（　　）

  A．25°

  B．40°

  C．45°

  D．50°
  組卷：981引用：6難度：0.9

  解析

• 9．利用勾股定理，可以作出長為無理數的線段．如圖，在數軸上找到點A，使OA=5，過點A作直線l垂直于OA，在l上取點B，使AB=2，以原點O為圓心，以OB長為半徑作弧，弧與數軸的交點為C，那么點C表示的無理數是（　　）

  A． 21

  B． 29

  C．7

  D．29
  組卷：1597引用：24難度：0.8

  解析

三、解答題（共64分，第19題10分，第20，22題7分，第21，23題，每題8分，第24題6分，第25，26題，每題9分）

• 26．如圖，在正方形ABCD中，E是邊AB上的一動點（不與點A、B重合），連接DE，點A關于直線DE的對稱點為F，連接EF并延長交BC于點G，連接DG，過點E作EH⊥DE交DG的延長線于點H，連接BH．
  （1）求證：GF=GC；
  （2）用等式表示線段BH與AE的數量關系，并證明．
  組卷：12281引用：22難度：0.4

  解析

• 27．附加：
  在平面直角坐標系中，對于兩個點P，Q和圖形W，如果在圖形W上存在點M，N（M，N可以重合）使得PM=QN，那么稱點P與點Q是圖形W的一對平衡點．
  （1）如圖1，已知點A（0，3），B（2，3）．
  ①設點O與線段AB上一點的距離為d,d的最小值是

  ，最大值是

  ；
  ②在p₁（

  3

  2

  ，

  0

  ）p₂（1，4）p₃（-3，0）這三個點中，與點O是線段 AB的一對平衡點的是

  ；
  （2）如圖2，已知正方形的邊長為2，一邊平行于x軸，對角線的交點為點O，點D的坐標為（2，0）．若點E（x,2）在第一象限，且點D與點E是正方形的一對平衡點，直接寫出x的取值范圍；
  （3）已知點F（-2，0），G（0，2），某正方形對角線的交點為坐標原點，邊長為a（0＜a≤2）．若線段FG上的任意兩個點都是此正方形的一對平衡點，直接寫出a的取值范圍．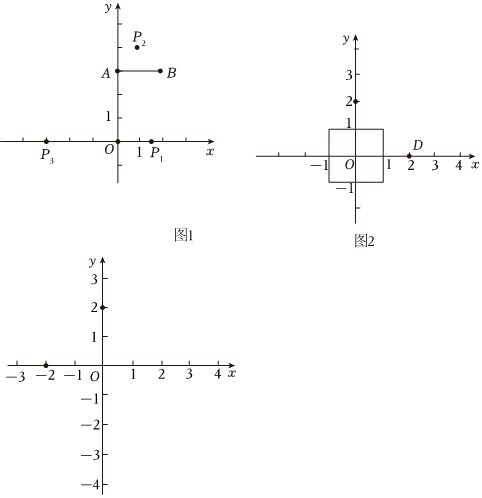
  ?
  組卷：214引用：1難度：0.1

  解析