2022-2023學年遼寧省鞍山市高一（下）期中數學試卷

一、單項選擇題：本題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.

• 1．tan210°=（　　）

  A． 3 3

  B． - 3 3

  C． 3

  D． - 3
  組卷：143引用：5難度：0.9

  解析

• 2．正△ABC的邊長為1，則

  AB

  ?

  BC

  =（　　）

  A． 1 2

  B．- 1 2

  C． 3 2

  D．- 3 2
  組卷：148引用：5難度：0.9

  解析

• 3．已知

  a

  ，

  b

  均為單位向量，它們的夾角為120°，則

  |

  3

  a

  +

  b

  |

  =（　　）

  A． 7

  B．7

  C． 13

  D．13
  組卷：658引用：4難度：0.7

  解析

• 4．把函數y=sinx的圖象上所有點的橫坐標縮短到原來的

  1

  2

  （縱坐標不變），再把圖象上所有的點向左平行移動

  π

  3

  個單位長度，得到的圖象所表示的函數是（　　）

  A． y = sin （ 2 x - π 3 ）	B． y = sin （ x 2 + π 6 ）
  C． y = sin （ 2 x + π 3 ）	D． y = sin （ 2 x + 2 π 3 ）
  組卷：98引用：5難度：0.6

  解析

• 5．已知

  sin

  （

  π

  6

  +

  α

  ）

  =

  3

  2

  ，則

  sin

  （

  5

  π

  6

  -

  α

  ）

  的值為（　　）

  A． 3 2

  B． - 3 2

  C． 1 2

  D． - 1 2
  組卷：133引用：2難度：0.8

  解析

• 6．已知非零向量

  a

  ，

  b

  ，

  c

  ，則“

  a

  ?

  c

  =

  b

  ?

  c

  ”是“

  a

  =

  b

  ”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充分必要條件	D．既不充分也不必要條件
  組卷：3614引用：38難度：0.8

  解析

• 7．已知單位向量

  a

  ，

  b

  的夾角為60°，則在下列向量中，與

  b

  垂直的是（　　）

  A． a + 2 b

  B．2 a + b

  C． a -2 b

  D．2 a - b
  組卷：6378引用：31難度：0.8

  解析

四、解答題：本題共6小題，共70分.解答應寫出必要的文字說明、證明過程及演算步驟.

• 21．設函數

  f

  （

  x

  ）

  =

  2

  3

  co

  s

  2

  x

  +

  （

  sinx

  -

  cosx

  ）

  2

  -

  1

  ．
  （1）求f（x）的最小正周期和最小值；
  （2）若

  g

  （

  x

  ）

  =

  f

  （

  3

  4

  π

  -

  1

  2

  x

  ）

  ，求g（x）的單調遞增區間．
  組卷：126引用：3難度：0.6

  解析

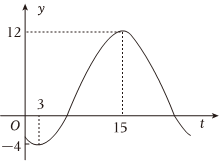• 22．建設生態文明是關系人民福祉、關乎民族未來的長遠大計．某市通宵營業的大型商場，為響應國家節能減排的號召，在氣溫低于0℃時，才開放中央空調，否則關閉中央空調．如圖是該市冬季某一天的氣溫（單位：℃）隨時間t（0≤t≤24，單位：小時）的大致變化曲線，若該曲線近似滿足

  f

  （

  t

  ）

  =

  A

  sin

  （

  ωt

  -

  3

  π

  4

  ）

  +

  b

  （

  A

  ＞

  0

  ，

  ω

  ＞

  0

  ）

  關系．
  （1）求y=f（t）的表達式；
  （2）請根據（1）的結論，求該商場的中央空調在一天內開啟的時長．
  組卷：85引用：2難度：0.6

  解析