2021-2022學年上海師大附中閔行區分校高一（下）期末數學試卷

一、填空題（本大題滿分54分）本大題共有12題，其中1-6每題4分，7-12每題5分．只要求直接填寫結果．

• 1．已知△ABC中

  |

  AB

  |

  =

  3

  ，

  |

  BC

  |

  =

  4

  ，

  |

  CA

  |

  =

  5

  ，求

  AB

  ?

  BC

  +

  BC

  ?

  CA

  +

  CA

  ?

  AB

  的值

  ．
  組卷：64引用：1難度：0.8

  解析

• 2．若復數

  1

  +

  i

  1

  -

  i

  +

  1

  2

  b

  （b∈R）的實部與虛部相等，則實數b的值為

  ．
  組卷：303引用：11難度：0.9

  解析

• 3．若三個平面兩兩相交，且三條交線互相平行，則這三個平面把空間分成

  部分．
  組卷：187引用：5難度：0.7

  解析

• 4．如果復數z滿足|z-1|+|z+1|=2，那么|z-1-i|的最大值是

  ．
  組卷：95引用：1難度：0.8

  解析

• 5．在正方體ABCD-A₁B₁C₁D₁中，與BD所成的角度為60°的棱或面對角線有

  條．
  組卷：31引用：1難度：0.6

  解析

• 6．已知θ為實數，若復數

  z

  =

  sinθ

  -

  1

  +

  i

  （

  2

  cosθ

  -

  1

  ）

  是純虛數，則z的虛部為

  ．
  組卷：64引用：1難度：0.7

  解析

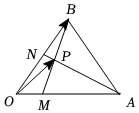• 7．如圖，△ABC中已知

  OA

  =

  a

  ，

  OB

  =

  b

  ，

  OM

  =

  1

  3

  a

  ，

  ON

  =

  1

  2

  b

  ，則用向量

  a

  ，

  b

  表示

  OP

  =

  ．
  組卷：125引用：1難度：0.7

  解析

三、解答題（本大題滿分76分）本大題共有5題，解答下列各題必須寫出必要的步驟，答題務必寫在答題紙上規定位置．

• 20．在△ABC中，AB=2，AC=3，O為三角形ABC的外心．
  （1）

  BC

  =

  10

  ，求

  AB

  ?

  AC

  ；
  （2）

  AO

  =

  x

  ?

  AB

  +

  y

  ?

  AC

  （

  x

  ,

  y

  ≠

  0

  ）

  ，且x+2y=1，求cos∠BAC；
  （3）在（1）條件下，

  AO

  =

  p

  ?

  AB

  +

  q

  ?

  AC

  ，求p、q的值．
  組卷：165引用：1難度：0.3

  解析

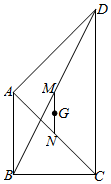• 21．如圖，在四邊形ABCD中，G為對角線AC與BD中點連線MN的中點，P為平面上任意給定的一點．
  （1）求證：

  4

  PG

  =

  PA

  +

  PB

  +

  PC

  +

  PD

  ；
  （2）若

  AB

  ?

  BC

  =

  BC

  ?

  CD

  =

  0

  ，

  |

  AB

  |

  =

  1

  ，

  |

  BC

  |

  =

  1

  ，

  |

  CD

  |

  =

  2

  ，點E在直線AD上運動，當E在什么位置時，

  |

  EG

  |

  取到最小值？
  （3）在（2）的條件下，過G的直線分別交線段AB、CD于點H、K（不含端點），若

  BH

  =

  m

  BA

  ，

  CK

  =

  n

  CD

  ，求

  1

  m

  +

  1

  n

  的最小值．
  組卷：143引用：2難度：0.4

  解析