香蕉视频国产精品,欧美精品一卡,亚洲综合国产精品

當前位置：章節挑題

請展開查看知識點列表

人教版：九年級上

教材版本: 人教版人教版（2024）北師大版北師大版（2024）華東師大版華東師大版（2024）蘇科版蘇科版（2024）湘教版湘教版（2024）青島版青島版（2024）浙教版浙教版（2024）冀教版冀教版（2024）滬科版滬科版（2024）魯教五四版魯教五四版（2024）北京課改版北京課改版（2024）滬教五四版滬教五四版（2024）人教五四版人教五四版（2024）

年級: 七年級上七年級下八年級上八年級下九年級上九年級下

第21章一元二次方程
第22章二次函數
第23章旋轉
第24章圓
第25章概率初步

更多>>

原創

更新中

《黃金講練》2024-2025學年人教版（2024）七下同步課堂

知識圖解新知探究答疑解惑針對訓練

瀏覽次數：5998 更新：2025年06月05日

原創

已完結

【解題模型】2024-2025學年人教版（2024）七下

解題模型因材施教夯實基礎穩步提升

瀏覽次數：13150 更新：2025年06月04日

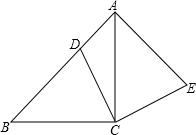2771．如圖，在△ABC中，∠ACB=90°，AC=BC，點D在邊AB上，連接CD，將線段CD繞點C順時針旋轉90°至CE位置，連接AE．
（1）求證：AB⊥AE；
（2）若BC²=AD?AB，求證：四邊形ADCE為正方形．
發布：2024/6/27 10:35:59組卷：818引用：71難度：0.5
解析
2772．如圖，已知AB是⊙O的直徑，C，D是⊙O上的點，OC∥BD，交AD于點E，連接BC．
（1）求證：AE=ED；
（2）若AB=6，∠ABC=30°，求圖中陰影部分的面積．
發布：2024/6/27 10:35:59組卷：2035引用：14難度：0.6
解析
2773．在平面直角坐標系中，拋物線y=x²+（k-1）x-k與直線y=kx+1交于A，B兩點，點A在點B的左側．
（1）如圖1，當k=1時，直接寫出A，B兩點的坐標；
（2）在（1）的條件下，點P為拋物線上的一個動點，且在直線AB下方，試求出△ABP面積的最大值及此時點P的坐標；
（3）如圖2，拋物線y=x²+（k-1）x-k（k＞0）與x軸交于點C、D兩點（點C在點D的左側），在直線y=kx+1上是否存在唯一一點Q，使得∠OQC=90°？若存在，請求出此時k的值；若不存在，請說明理由．
發布：2024/6/27 10:35:59組卷：6581引用：72難度：0.1
解析
2774．閱讀下列材料：
（1）將一個多項式化成幾個整式的積的形式，像這樣的式子變形，叫做這個多項式的因式分解：例如a²-b²=（a+b）（a-b）；
（2）我們把多項式a²+2ab+b²及a²-2ab+b²叫做完全平方式，如果一個多項式不是完全平方式，我們常做如下變形：先添加一個適當的項，使式子中出現完全平方式，再減去這個項，使整個式子的值不變，這種方法叫做配方法；
配方法是一種重要的解決問題的數學方法，不僅可以將一個看似不能分解的多項式分解因式，還能解決一些與非負數有關的問題或求代數式最大值，最小值等．
例如：分解因式
x²+2x-3=（x²+2x+1）-4=（x+1）²-4=（x+1+2）（x+1-2）=（x+3）（x-1）；
再例如求代數式2x²+4x-6的最小值．2x²+4x-6=2（x²+2x-3）=2（x+1）²-8．可知當x=-1時，2x²+4x-6有最小值，最小值是-8，根據閱讀材料用配方法解決下列問題：
（1）分解因式：m²-4m-5；
（2）當a,b為何值時，多項式a²+b²-4a+6b+18有最小值，并求出這個最小值；
（3）已知a,b,c為△ABC的三邊，且滿足a²+2b²+c²-2b（a+c）=0，試判斷此三角形的形狀．
發布：2024/6/27 10:35:59組卷：503引用：2難度：0.7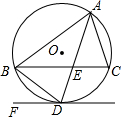
解析
2775．如圖，⊙O是△ABC的外接圓，∠BAC的平分線交⊙O于點D，交BC于點E，過點D作直線DF∥BC．
（1）判斷直線DF與⊙O的位置關系，并說明理由；
（2）若AB=6，AE=
12
3
5
，CE=
4
7
5
，求BD的長．
發布：2024/6/27 10:35:59組卷：1744引用：6難度：0.5
解析
2776．如圖，在△ABC中，AB=BC=2，∠ABC=90°，則圖中陰影部分的面積是

．
發布：2024/6/27 10:35:59組卷：3055引用：60難度：0.5
解析
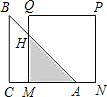2777．如圖，已知等腰直角三角形ABC的直角邊長與正方形MNPQ的邊長均為20cm,AC與MN在同一條直線上，開始時點A與點N重合，讓△ABC以2cm/s的速度向左運動，最終點A與點M重合，求重疊部分的面積ycm²與時間ts之間的函數關系式．
發布：2024/6/27 10:35:59組卷：1207引用：5難度：0.5
解析
2778．大潤發超市銷售某廠家生產的A型智能手機，從廠家按出廠價800元/部進貨，然后標價1200元/部銷售，平均每天可售出10部．國慶七天假期，廠家和超市聯合促銷．廠家對超市承諾：在七天促銷期間銷售的A型智能手機的出廠價每部優惠50元；對多銷的部分，廠家每部再優惠50元．超市經過調查發現，若每部手機降價40元，平均每天可多售4部手機．
（1）若超市國慶期間某天售出10部手機，則每部A型智能手機的進貨價是
．
（2）最后經統計，在這七天中，通過降價銷售及廠家讓利，超市銷售A型智能手機共獲得的總利潤為58380元，且能讓顧客盡可能得到實惠．那國慶期間超市確定的A型智能手機的銷售單價是多少？
發布：2024/6/27 10:35:59組卷：197引用：3難度：0.3
解析
2779．已知拋物線y=2x²+n與直線y=2x-1交于點（m,3）．
（1）求m和n的值；
（2）求拋物線y=2x²+n的頂點坐標和對稱軸；
（3）當x取何值時，二次函數y=2x²+n中y隨x的增大而減小；
（4）函數y=2x²+n與直線y=2x-1的圖象是否還有其他交點？若有，請求出來；若沒有，請說明理由．
發布：2024/6/27 10:35:59組卷：506引用：5難度：0.6
解析
2780．設二次函數y=ax²+bx-（a+b）（a,b是常數，a≠0）．
（1）判斷該二次函數圖象與x軸的交點的個數，說明理由．
（2）若該二次函數圖象經過A（-1，4），B（0，-1），C（1，1）三個點中的其中兩個點，求該二次函數的表達式．
（3）若a+b＜0，點P（2，m）（m＞0）在該二次函數圖象上，求證：a＞0．
發布：2024/6/27 10:35:59組卷：8410引用：12難度：0.3
解析

首頁上一頁 …277 278 279 280 …下一頁尾頁

2771．如圖，在△ABC中，∠ACB=90°，AC=BC，點D在邊AB上，連接CD，將線段CD繞點C順時針旋轉90°至CE位置，連接AE．（1）求證：AB⊥AE；（2）若BC2=AD?AB，求證：四邊形ADCE為正方形．

2772．如圖，已知AB是⊙O的直徑，C，D是⊙O上的點，OC∥BD，交AD于點E，連接BC．（1）求證：AE=ED；（2）若AB=6，∠ABC=30°，求圖中陰影部分的面積．

2775．如圖，⊙O是△ABC的外接圓，∠BAC的平分線交⊙O于點D，交BC于點E，過點D作直線DF∥BC．（1）判斷直線DF與⊙O的位置關系，并說明理由；（2）若AB=6，AE=1235，CE=475，求BD的長．

2776．如圖，在△ABC中，AB=BC=2，∠ABC=90°，則圖中陰影部分的面積是 ．

2777．如圖，已知等腰直角三角形ABC的直角邊長與正方形MNPQ的邊長均為20cm,AC與MN在同一條直線上，開始時點A與點N重合，讓△ABC以2cm/s的速度向左運動，最終點A與點M重合，求重疊部分的面積ycm2與時間ts之間的函數關系式．

2771．如圖，在△ABC中，∠ACB=90°，AC=BC，點D在邊AB上，連接CD，將線段CD繞點C順時針旋轉90°至CE位置，連接AE．
（1）求證：AB⊥AE；
（2）若BC²=AD?AB，求證：四邊形ADCE為正方形．

2772．如圖，已知AB是⊙O的直徑，C，D是⊙O上的點，OC∥BD，交AD于點E，連接BC．
（1）求證：AE=ED；
（2）若AB=6，∠ABC=30°，求圖中陰影部分的面積．

2775．如圖，⊙O是△ABC的外接圓，∠BAC的平分線交⊙O于點D，交BC于點E，過點D作直線DF∥BC．
（1）判斷直線DF與⊙O的位置關系，并說明理由；
（2）若AB=6，AE=
12
3
5
，CE=
4
7
5
，求BD的長．

2776．如圖，在△ABC中，AB=BC=2，∠ABC=90°，則圖中陰影部分的面積是

．

2777．如圖，已知等腰直角三角形ABC的直角邊長與正方形MNPQ的邊長均為20cm,AC與MN在同一條直線上，開始時點A與點N重合，讓△ABC以2cm/s的速度向左運動，最終點A與點M重合，求重疊部分的面積ycm²與時間ts之間的函數關系式．