當前位置：試卷中心 > 試卷詳情

2019-2020學年河南省許昌市高一（下）期末數學試卷（文科）

發布：2025/6/28 23:0:12

一、選擇題：本題共12小題，每小題5分，共60分。在每小題給出的四個選項中，只有一項是符合題目要求的。

1．中國運動員谷愛凌在2022北京冬奧會自由式滑雪女子大跳臺決賽中以188.25分奪得金牌．自由式滑雪大跳臺比賽一般有資格賽和決賽兩個階段，比賽規定：資格賽前12名進入決賽．在某次自由式滑雪大跳臺比賽中，24位參加資格賽選手的成績各不相同．如果選手甲知道了自己的成績后，則他可根據其他23位同學成績的哪個數據判斷自己能否進入決賽（　　）
A．中位數 B．極差 C．平均數 D．方差
組卷：146引用：2難度：0.7
解析
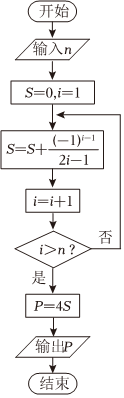2．德國數學家萊布尼茲于1674年得到了第一個關于π的級數展開式，該公式于明朝初年傳入我國．我國數學家、天文學家明安圖為提高我國的數學研究水平，從乾隆初年（1736年）開始，歷時近30年，證明了包括這個公式在內的三個公式，同時求得了展開三角函數和反三角函數的6個新級數公式，著有《割圓密率捷法》一書，為我國用級數計算π開創先河，如圖所示的程序框圖可以用萊布尼茲“關于的級數展開式計算π的近似值（其中P表示π的近似值）．若輸入n=8，輸出的結果P可以表示（　　）
A．P=4（1-
1
3
+
1
5
-
1
7
+…-
1
11
）
B．P=4（1-
1
3
+
1
5
-
1
7
+…+
1
13
）
C．P=4（1-
1
3
+
1
5
-
1
7
+…-
1
15
）
D．P=4（1-
1
3
+
1
5
-
1
7
+…+
1
17
）
組卷：31引用：3難度：0.6
解析
3．已知
a
，
b
為平面上的單位向量，“
a
⊥
b
”是“
|
3
a
+
2
b
|
=
|
2
a
-
3
b
|
”的（　　）
A．充分而不必要條件 B．必要而不充分條件
C．充分必要條件 D．既不必要又不充分條件
組卷：144引用：3難度：0.8
解析
4．已知向量
a
=
（
t
2
+
1
，
4
）
，
b
=
（
2
，
t
）
，
c
=
（
3
，
4
）
，當
a
?
b
取最小值時，
b
?
c
=（　　）
A．5 B．4 C．3 D．2
組卷：97引用：2難度：0.7
解析
5．在平行四邊形ABCD中，AC與BD交于點O，
CO
=3
CE
，BE的延長線與CD交于點F．若
AB
=
a
，
AD
=
b
，則
EF
=（　　）
A．
6
7
a
-
1
6
b
B．-
1
30
a
+
1
6
b
C．
1
30
a
+
1
6
b
D．
6
7
a
+
1
6
b
組卷：585引用：3難度：0.5
解析
6．已知
f
（
x
）
=
3
sin
（
ωx
+
?
）
-
cos
（
ωx
+
?
）
（
ω
＞
0
，
|
?
|
＜
π
2
）
的最小正周期為π，將f（x）的圖象向右平移
π
12
個單位后得到的圖象關于y軸對稱，則函數f（x）的減區間為（　　）
A．
[
kπ
-
π
12
，
kπ
+
5
π
12
]
，
k
∈
Z
B．
[
kπ
+
π
6
，
kπ
+
2
π
3
]
，
k
∈
Z
C．
[
kπ
+
5
π
12
，
kπ
+
11
π
12
]
，
k
∈
Z
D．
[
kπ
-
π
3
，
kπ
+
π
6
]
，
k
∈
Z
組卷：45引用：1難度：0.9
解析
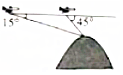7．航空測量組的飛機航線和山頂在同一鉛直平面內，已知飛機的高度為海拔10千米，速度為180千米/小時，飛機先看到山頂的俯角為15°，經過420秒后又看到山頂的俯角為45°，則山頂的海拔高度為（取
2
=
1
.
4
，
3
=
1
.
7
）（　　）
A．2.65千米 B．7.35千米 C．10千米 D．10.5千米
組卷：31引用：1難度：0.7
解析
8．設函數f（x）=2sin（2x+
π
6
）的最小正周期為T，將f（x）的圖象向右平移
T
3
個單位后，所得圖象（　　）
A．關于點（
π
4
，0）對稱 B．關于點（
π
3
，0）對稱
C．關于點（
7
π
12
，0）對稱 D．關于點（-
5
π
12
，0）對稱
組卷：99引用：5難度：0.6
解析
9．已知一組數據2x₁-3，2x₂-3，2x₃-3，2x₄-3，2x₅-3的平均數是1，那么另一組數據x₁，x₂，x₃，x₄，x₅的平均數為（　　）
A．4 B．3 C．2 D．1
組卷：298引用：3難度：0.8
解析
10．tan300°的值為（　　）
A．
3
3
B．-
3
C．
3
D．-
3
3
組卷：790引用：17難度：0.9
解析
11．系統找不到該試題
12．系統找不到該試題

二、填空題：本大題共4小題，每小題5分，滿分20分。

13．《易經》中記載著一種幾何圖形--八封圖，圖中正八邊形代表八卦，中間的圓代表陰陽太極圖，圖中八塊面積相等的曲邊梯形代表八卦田．某中學開展勞動實習，去測量當地八卦田的面積如圖，現測得正八邊形的過長為8m,代表陰陽太極圖的圓的半徑為2m,則每塊八卦田的面積為
m²．
組卷：94引用：4難度：0.6
解析
14．已知平面向量
a
=
（
1
，
cosθ
）
，
b
=
（
sinθ
，-
2
）
，且
a
⊥
b
，
則
tan
（
π
+
θ
）
=
．
組卷：23引用：2難度：0.7
解析
15．在三棱錐S-ABC內任取一點P，使得
V
P
-
ABC
＞
2
3
V
S
-
ABC
的概率是
．
組卷：1引用：2難度：0.6
解析
16．某校有高一、高二、高三、三個年級，其人數之比為2：2：1，現用分層抽樣的方法從總體中抽取一個容量為10的樣本，現從所抽取樣本中選兩人做問卷調查，至少有一個是高一學生的概率為
．
組卷：89引用：1難度：0.7
解析

三、解答題：本大題共6個小題，共70分。解答應寫出文字說明、證明過程或演算步驟。

17．已知函數
f
（
x
）
=
2
sin
（
x
+
π
3
）
?
cosx
．
（1）若f（x）=0，求x的取值集合；
（2）若函數f（x）的圖像向右平移
π
3
個單位，再把得到圖像上所有點的縱坐標不變，橫坐標伸長4倍得到函數g（x）的圖像，求函數g（x）的單調遞增區間．
組卷：42引用：1難度：0.5
解析
18．已知銳角△ABC中，a,b,c分別為內角A，B，C的對邊，若sinAsinBsinC=
3
2
（sin²A+sin²B-sin²C）．
（1）求sinC；
（2）若c=
3
，求△ABC周長的取值范圍．
組卷：554引用：2難度：0.6
解析
19．設函數
f
（
x
）
=
sin
（
2
x
+
π
3
）
+
3
si
n
2
x
-
3
co
s
2
x
-
1
2

（1）求f（x）的最小正周期及其圖像的對稱中心；
（2）若
x
0
∈
[
5
π
12
，
2
π
3
]
且
f
（
x
0
）
=
3
3
-
1
2
，求cos2x₀的值．
組卷：210引用：2難度：0.6
解析
20．已知函數f（x）=Asin（ωx+φ）（A＞0，ω＞0）．
（Ⅰ）若將f（x）圖象上所有點的橫坐標縮短為原來的
1
2
（縱坐標不變），再將所得圖象向上平移1個單位得到g（x）的圖象，且g（x）的圖象關于y軸對稱，求φ的最小正值；
（Ⅱ）如圖，函數f（x）的圖象與y軸的交點為M（0，1），與x軸正半軸最靠近y軸的交點為N（3，0），y軸右側第一個最高點和第一個最低點分別為B，C，其中△OBC（O為坐標原點）的面積為
3
2
．
|
?
|
＜
π
2
，求f（x）的解析式，以及f（x）的最小正周期．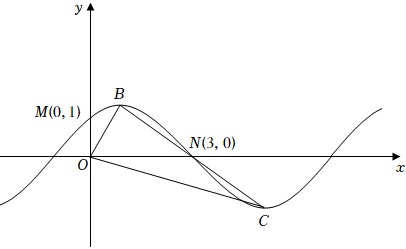
組卷：129引用：1難度：0.6
解析
21．已知函數
f
（
x
）
=
（
2
3
sinx
+
2
cosx
）
cosx
+
m
-
1
，
（1）求函數f（x）的最小正周期和單調增區間；
（2）若函數f（x）在區間
[
-
π
12
，
π
2
]
上的最小值為0，求實數m的值；
（3）若
f
（
θ
2
）
=
6
3
+
m
，求
sin
（
2
θ
-
π
6
）
的值．
組卷：11引用：1難度：0.5
解析
22．解方程：cos²x+cos²2x+cos²3x=1．
組卷：146引用：1難度：0.5
解析

0/60 進入組卷

0/20 進入試卷籃

布置作業 發布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

A．充分而不必要條件	B．必要而不充分條件
C．充分必要條件	D．既不必要又不充分條件

A． [ kπ - π 12 ， kπ + 5 π 12 ] ， k ∈ Z	B． [ kπ + π 6 ， kπ + 2 π 3 ] ， k ∈ Z
C． [ kπ + 5 π 12 ， kπ + 11 π 12 ] ， k ∈ Z	D． [ kπ - π 3 ， kπ + π 6 ] ， k ∈ Z

A．關于點（ π 4 ，0）對稱	B．關于點（ π 3 ，0）對稱
C．關于點（ 7 π 12 ，0）對稱	D．關于點（- 5 π 12 ，0）對稱

2019-2020學年河南省許昌市高一（下）期末數學試卷（文科）

一、選擇題：本題共12小題，每小題5分，共60分。在每小題給出的四個選項中，只有一項是符合題目要求的。

3．已知a，b為平面上的單位向量，“a⊥b”是“|3a+2b|=|2a-3b|”的（ ）

4．已知向量a=（t2+1，4），b=（2，t），c=（3，4），當a?b取最小值時，b?c=（ ）

5．在平行四邊形ABCD中，AC與BD交于點O，CO=3CE，BE的延長線與CD交于點F．若AB=a，AD=b，則EF=（ ）

6．已知f（x）=3sin（ωx+?）-cos（ωx+?）（ω＞0，|?|＜π2）的最小正周期為π，將f（x）的圖象向右平移π12個單位后得到的圖象關于y軸對稱，則函數f（x）的減區間為（ ）

7．航空測量組的飛機航線和山頂在同一鉛直平面內，已知飛機的高度為海拔10千米，速度為180千米/小時，飛機先看到山頂的俯角為15°，經過420秒后又看到山頂的俯角為45°，則山頂的海拔高度為（取2=1.4，3=1.7）（ ）

8．設函數f（x）=2sin（2x+π6）的最小正周期為T，將f（x）的圖象向右平移T3個單位后，所得圖象（ ）

9．已知一組數據2x1-3，2x2-3，2x3-3，2x4-3，2x5-3的平均數是1，那么另一組數據x1，x2，x3，x4，x5的平均數為（ ）

10．tan300°的值為（ ）

二、填空題：本大題共4小題，每小題5分，滿分20分。

14．已知平面向量a=（1，cosθ），b=（sinθ，-2），且a⊥b，則tan（π+θ）=．

15．在三棱錐S-ABC內任取一點P，使得VP-ABC＞23VS-ABC的概率是 ．

16．某校有高一、高二、高三、三個年級，其人數之比為2：2：1，現用分層抽樣的方法從總體中抽取一個容量為10的樣本，現從所抽取樣本中選兩人做問卷調查，至少有一個是高一學生的概率為 ．

三、解答題：本大題共6個小題，共70分。解答應寫出文字說明、證明過程或演算步驟。

17．已知函數f（x）=2sin（x+π3）?cosx．（1）若f（x）=0，求x的取值集合；（2）若函數f（x）的圖像向右平移π3個單位，再把得到圖像上所有點的縱坐標不變，橫坐標伸長4倍得到函數g（x）的圖像，求函數g（x）的單調遞增區間．

18．已知銳角△ABC中，a,b,c分別為內角A，B，C的對邊，若sinAsinBsinC=32（sin2A+sin2B-sin2C）．（1）求sinC；（2）若c=3，求△ABC周長的取值范圍．

19．設函數f（x）=sin（2x+π3）+3sin2x-3cos2x-12（1）求f（x）的最小正周期及其圖像的對稱中心；（2）若x0∈[5π12，2π3]且f（x0）=33-12，求cos2x0的值．

21．已知函數f（x）=（23sinx+2cosx）cosx+m-1，（1）求函數f（x）的最小正周期和單調增區間；（2）若函數f（x）在區間[-π12，π2]上的最小值為0，求實數m的值；（3）若f（θ2）=63+m，求sin（2θ-π6）的值．

22．解方程：cos2x+cos22x+cos23x=1．

3．已知
a
，
b
為平面上的單位向量，“
a
⊥
b
”是“
|
3
a
+
2
b
|
=
|
2
a
-
3
b
|
”的（　　）

4．已知向量
a
=
（
t
2
+
1
，
4
）
，
b
=
（
2
，
t
）
，
c
=
（
3
，
4
）
，當
a
?
b
取最小值時，
b
?
c
=（　　）

5．在平行四邊形ABCD中，AC與BD交于點O，
CO
=3
CE
，BE的延長線與CD交于點F．若
AB
=
a
，
AD
=
b
，則
EF
=（　　）

6．已知
f
（
x
）
=
3
sin
（
ωx
+
?
）
-
cos
（
ωx
+
?
）
（
ω
＞
0
，
|
?
|
＜
π
2
）
的最小正周期為π，將f（x）的圖象向右平移
π
12
個單位后得到的圖象關于y軸對稱，則函數f（x）的減區間為（　　）

8．設函數f（x）=2sin（2x+
π
6
）的最小正周期為T，將f（x）的圖象向右平移
T
3
個單位后，所得圖象（　　）

9．已知一組數據2x₁-3，2x₂-3，2x₃-3，2x₄-3，2x₅-3的平均數是1，那么另一組數據x₁，x₂，x₃，x₄，x₅的平均數為（　　）

10．tan300°的值為（　　）

14．已知平面向量
a
=
（
1
，
cosθ
）
，
b
=
（
sinθ
，-
2
）
，且
a
⊥
b
，
則
tan
（
π
+
θ
）
=
．

15．在三棱錐S-ABC內任取一點P，使得
V
P
-
ABC
＞
2
3
V
S
-
ABC
的概率是
．

16．某校有高一、高二、高三、三個年級，其人數之比為2：2：1，現用分層抽樣的方法從總體中抽取一個容量為10的樣本，現從所抽取樣本中選兩人做問卷調查，至少有一個是高一學生的概率為
．

18．已知銳角△ABC中，a,b,c分別為內角A，B，C的對邊，若sinAsinBsinC=
3
2
（sin²A+sin²B-sin²C）．
（1）求sinC；
（2）若c=
3
，求△ABC周長的取值范圍．

19．設函數
f
（
x
）
=
sin
（
2
x
+
π
3
）
+
3
si
n
2
x
-
3
co
s
2
x
-
1
2

（1）求f（x）的最小正周期及其圖像的對稱中心；
（2）若
x
0
∈
[
5
π
12
，
2
π
3
]
且
f
（
x
0
）
=
3
3
-
1
2
，求cos2x₀的值．

22．解方程：cos²x+cos²2x+cos²3x=1．