當前位置：試卷中心 > 試卷詳情

2021-2022學年重慶市三峽名校聯盟高二（下）聯考數學試卷（5月份）

發布：2025/6/29 0:0:12

一、選擇題（共8小題，每小題5分，滿分40分）

1．已知（
x
-
2
x
）ⁿ的展開式中各項的二項式系數的和為512，則這個展開式中的常數項為（　　）
A．-34 B．-672 C．84 D．672
組卷：378引用：3難度：0.7
解析
2．已知集合A={1，2，3，4}，B={5，6，7}，C={8，9}．現在從這三個集合中取出兩個集合，再從這兩個集合中各取出一個元素，組成一個含有兩個元素的集合，則一共可以組成多少個集合（　　）
A．24個 B．36個 C．26個 D．27個
組卷：1063引用：4難度：0.9
解析
3．函數
y
=
cosx
x
的圖象大致為（　　）
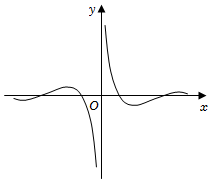
A． B．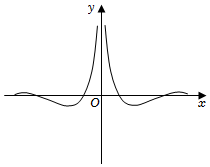
C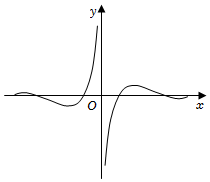． D．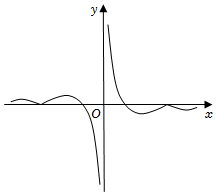
組卷：82引用：2難度：0.6
解析
4．某學校需要把包含甲、乙、丙在內的6名教育專家安排到高一、高二、高三三個年級去聽課，每個年級安排2名專家，已知甲必須安排到高一年級，乙和丙不能安排到同一年級，則安排方案的種數有（　　）
A．24種 B．36種 C．48種 D．72種
組卷：149引用：2難度：0.8
解析
5．已知函數f（x）滿足f（x）=2f'（1）lnx+
x
e
（f'（x）為f（x）的導函數），則f（e）=（　　）
A．e-1 B．
2
e
+
1
C．1 D．
-
2
e
+
1
組卷：223引用：4難度：0.8
解析
6．盒中有2個紅球，3個黑球，2個白球，從中隨機地取出一個球，觀察其顏色后放回，并加入同色球1個，再從盒中抽取一球，則第二次抽出的是紅球的概率是（　　）
A．
2
7
B．
7
28
C．
3
7
D．
19
56
組卷：363引用：7難度：0.7
解析
7．已知函數f（x）在x=x₀處的導數為f′（x₀），則
lim
Δ
x
→
0
f
（
x
0
+
Δ
x
）
-
f
（
x
0
）
2
Δ
x
=（　　）
A．2f′（x₀） B．-2f′（x₀） C．
1
2
f
′
（
x
0
）
D．
-
1
2
f
′
（
x
0
）
組卷：70引用：6難度：0.8
解析
8．若函數f（x）=ke^x-
1
2
x²在區間（0，+∞）上單調遞增，則實數k的取值范圍是（　　）
A．[
1
e
，+∞） B．（0，+∞） C．（
1
e
，+∞） D．[0，+∞）
組卷：820引用：6難度：0.9
解析

二、選擇題（共4小題，每小題5分，滿分20分）

9．甲、乙、丙、丁、戊5人參加完某項活動后合影留念，則（　　）

A．甲、乙、丙站前排，丁、戊站后排，共有120種排法

B．5人站成一排，若甲、乙站一起且甲在乙的左邊，共有24種排法

C．5人站成一排，甲不在兩端，共有72種排法

D．5人站成一排，甲不在最左端，乙不在最右端，共有78種排法

組卷：51引用：2難度：0.5

解析

10．已知函數f（x）=-3x⁴+6x²-1，f′（x）是f（x）的導函數，且f′（a）=f′（b）=f′（c），其中a＜b＜c,則下列說法正確的是（　　）
A．f（x）的所有極值點之和為0
B．f（x）的極大值點之積為2
C．ab+ac+bc=-1
D．abc的取值范圍是
（
-
32
3
，
32
3
）
組卷：30引用：3難度：0.6
解析
11．已知正數α，β滿足
e
α
-
e
β
＞
1
2
α
+
sinα
-
1
2
β
+
sinβ
，則下列不等式正確的是（　　）
A．
1
α
+
1
β
＜
4
a
+
β
B．2^α-β+1＞2
C．lnα+α＜lnβ+β D．
1
e
a
+
1
α
＜
1
e
β
+
1
β
組卷：21引用：2難度：0.4
解析
12．
（
3
x
-
1
x
）
6
的展開式中，下列說法正確的是（　　）
A．所有項系數和為64 B．常數項為第4項
C．整式共有3項 D．x³項的系數-81
組卷：109引用：6難度：0.8
解析

三、填空題（共4小題，每小題5分，滿分20分）

13．設
f
（
x
）
=
|
x
+
1
x
|
+
|
1
-
1
x
|
，若存在a∈R使得關于x的方程（f（x））²+af（x）+b=0恰有六個解，則b的取值范圍是
．
組卷：332引用：7難度：0.5
解析
14．安排5名歌手的演出順序時，要求某名歌手不第一個出場，則不同排法的總數是
．（用數字作答）
組卷：33引用：1難度：0.6
解析
15．信息技術輔助教學已經成為教學的主流趨勢，為了了解學生利用學習機學習的情況，某研究機構在購物平臺上購買了6種主流的學習機，并安排4人進行相關數據統計，且每人至少統計1種學習機的相關數據（不重復統計），則不同的安排方法有
．
組卷：54引用：2難度：0.6
解析
16．下列4組函數：①y=x²；②y=2^x；③y=log₂x；④y=2x哪個函數增長速度最快
（填序號）
組卷：53引用：1難度：0.7
解析

四、解答題（共6小題，滿分70分）

17．從1到9這9個數字中取3個偶數和4個奇數，組成沒有重復數字的七位數，試問：
（1）能組成多少個這樣的七位數？
（2）3個偶數排在一起的七位數有多少個？
（3）任意2個偶數都不相鄰的七位數有多少個？
組卷：89引用：3難度：0.6
解析
18．甲、乙等五名深圳大運會志愿者被隨機地分到A，B，C，D四個不同的崗位服務，每個崗位至少有一名志愿者．
（Ⅰ）求甲、乙兩人同時參加A崗位服務的概率；
（Ⅱ）設隨機變量ξ為這五名志愿者中參加A崗位服務的人數，求ξ的分布列．
組卷：39引用：6難度：0.3
解析
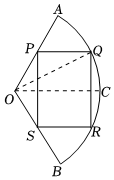19．今年2月底俄羅斯與烏克蘭沖突爆發以來，大量的烏克蘭人民離開故土開啟了逃亡之路，截止3月底，聯合國難民事務高級專員表示，烏克蘭難民人數已經超過400萬，其中大多數逃往波蘭、匈牙利、摩爾多瓦、羅馬尼亞和斯洛伐克等鄰國．各鄰國都在陸續建立難民收容所，波蘭某地準備在一個廢棄的汽車停車場，臨時建一處形狀為矩形的收容所供烏克蘭難民所用．已知停車場是近似如圖所示半徑為50米，圓心角為
2
π
3
的扇形區域AOB，C為弧
?
AB
的中點，設∠QOC=θ，
（1）用θ來表示矩形PQRS的面積f（θ），并指出θ的取值范圍；
（2）θ為多少時，f（θ）取得最大值，并求出此最大值．
組卷：36引用：3難度：0.6
解析
20．已知f（x）=e^x-1-a（x-1）．
（1）討論函數f（x）的單調性；
（2）若f（x）＞xlnx+ln
e
2
恒成立，求實數a的取值范圍．
組卷：44引用：1難度：0.2
解析
21．已知函數f（x）=-
1
2
x
2
+ax-lnx（a∈R）．
（1）當a=1時，求曲線y=f（x）在點（1，f（1））處的切線方程；
（2）求f（x）的單調區間；
（3）若函數f（x）有兩個極值點x₁，x₂（x₁＜x₂），求證：4f（x₁）-2f（x₂）≤1+3ln2．
組卷：440引用：9難度：0.3
解析
22．已知（
3
x
2
+3x）ⁿ展開式各項系數和比它的二項式系數和大992．
（1）求展開式中含有x⁴的項；
（2）求展開式中二項式系數最大的項；
（3）求展開式中系數最大的項．
組卷：414引用：8難度：0.5
解析

0/60 進入組卷

0/20 進入試卷籃

布置作業 發布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

A． 1 α + 1 β ＜ 4 a + β	B．2^α-β+1＞2
C．lnα+α＜lnβ+β	D． 1 e a + 1 α ＜ 1 e β + 1 β

A．所有項系數和為64	B．常數項為第4項
C．整式共有3項	D．x³項的系數-81

A．	B．
C．	D．

2021-2022學年重慶市三峽名校聯盟高二（下）聯考數學試卷（5月份）

一、選擇題（共8小題，每小題5分，滿分40分）

1．已知（x-2x）n的展開式中各項的二項式系數的和為512，則這個展開式中的常數項為（ ）

2．已知集合A={1，2，3，4}，B={5，6，7}，C={8，9}．現在從這三個集合中取出兩個集合，再從這兩個集合中各取出一個元素，組成一個含有兩個元素的集合，則一共可以組成多少個集合（ ）

3．函數y=cosxx的圖象大致為（ ）

4．某學校需要把包含甲、乙、丙在內的6名教育專家安排到高一、高二、高三三個年級去聽課，每個年級安排2名專家，已知甲必須安排到高一年級，乙和丙不能安排到同一年級，則安排方案的種數有（ ）

5．已知函數f（x）滿足f（x）=2f'（1）lnx+xe（f'（x）為f（x）的導函數），則f（e）=（ ）

6．盒中有2個紅球，3個黑球，2個白球，從中隨機地取出一個球，觀察其顏色后放回，并加入同色球1個，再從盒中抽取一球，則第二次抽出的是紅球的概率是（ ）

7．已知函數f（x）在x=x0處的導數為f′（x0），則limΔx→0f（x0+Δx）-f（x0）2Δx=（ ）

8．若函數f（x）=kex-12x2在區間（0，+∞）上單調遞增，則實數k的取值范圍是（ ）

二、選擇題（共4小題，每小題5分，滿分20分）

9．甲、乙、丙、丁、戊5人參加完某項活動后合影留念，則（ ）

10．已知函數f（x）=-3x4+6x2-1，f′（x）是f（x）的導函數，且f′（a）=f′（b）=f′（c），其中a＜b＜c,則下列說法正確的是（ ）

11．已知正數α，β滿足eα-eβ＞12α+sinα-12β+sinβ，則下列不等式正確的是（ ）

12．（3x-1x）6的展開式中，下列說法正確的是（ ）

三、填空題（共4小題，每小題5分，滿分20分）

13．設f（x）=|x+1x|+|1-1x|，若存在a∈R使得關于x的方程（f（x））2+af（x）+b=0恰有六個解，則b的取值范圍是 ．

14．安排5名歌手的演出順序時，要求某名歌手不第一個出場，則不同排法的總數是 ．（用數字作答）

16．下列4組函數：①y=x2；②y=2x；③y=log2x；④y=2x哪個函數增長速度最快 （填序號）

四、解答題（共6小題，滿分70分）

17．從1到9這9個數字中取3個偶數和4個奇數，組成沒有重復數字的七位數，試問：（1）能組成多少個這樣的七位數？（2）3個偶數排在一起的七位數有多少個？（3）任意2個偶數都不相鄰的七位數有多少個？

20．已知f（x）=ex-1-a（x-1）．（1）討論函數f（x）的單調性；（2）若f（x）＞xlnx+lne2恒成立，求實數a的取值范圍．

21．已知函數f（x）=-12x2+ax-lnx（a∈R）．（1）當a=1時，求曲線y=f（x）在點（1，f（1））處的切線方程；（2）求f（x）的單調區間；（3）若函數f（x）有兩個極值點x1，x2（x1＜x2），求證：4f（x1）-2f（x2）≤1+3ln2．

22．已知（3x2+3x）n展開式各項系數和比它的二項式系數和大992．（1）求展開式中含有x4的項；（2）求展開式中二項式系數最大的項；（3）求展開式中系數最大的項．

1．已知（
x
-
2
x
）ⁿ的展開式中各項的二項式系數的和為512，則這個展開式中的常數項為（　　）

2．已知集合A={1，2，3，4}，B={5，6，7}，C={8，9}．現在從這三個集合中取出兩個集合，再從這兩個集合中各取出一個元素，組成一個含有兩個元素的集合，則一共可以組成多少個集合（　　）

3．函數
y
=
cosx
x
的圖象大致為（　　）

4．某學校需要把包含甲、乙、丙在內的6名教育專家安排到高一、高二、高三三個年級去聽課，每個年級安排2名專家，已知甲必須安排到高一年級，乙和丙不能安排到同一年級，則安排方案的種數有（　　）

5．已知函數f（x）滿足f（x）=2f'（1）lnx+
x
e
（f'（x）為f（x）的導函數），則f（e）=（　　）

6．盒中有2個紅球，3個黑球，2個白球，從中隨機地取出一個球，觀察其顏色后放回，并加入同色球1個，再從盒中抽取一球，則第二次抽出的是紅球的概率是（　　）

7．已知函數f（x）在x=x₀處的導數為f′（x₀），則
lim
Δ
x
→
0
f
（
x
0
+
Δ
x
）
-
f
（
x
0
）
2
Δ
x
=（　　）

8．若函數f（x）=ke^x-
1
2
x²在區間（0，+∞）上單調遞增，則實數k的取值范圍是（　　）

9．甲、乙、丙、丁、戊5人參加完某項活動后合影留念，則（　　）

10．已知函數f（x）=-3x⁴+6x²-1，f′（x）是f（x）的導函數，且f′（a）=f′（b）=f′（c），其中a＜b＜c,則下列說法正確的是（　　）

11．已知正數α，β滿足
e
α
-
e
β
＞
1
2
α
+
sinα
-
1
2
β
+
sinβ
，則下列不等式正確的是（　　）

12．
（
3
x
-
1
x
）
6
的展開式中，下列說法正確的是（　　）

13．設
f
（
x
）
=
|
x
+
1
x
|
+
|
1
-
1
x
|
，若存在a∈R使得關于x的方程（f（x））²+af（x）+b=0恰有六個解，則b的取值范圍是
．

14．安排5名歌手的演出順序時，要求某名歌手不第一個出場，則不同排法的總數是
．（用數字作答）

16．下列4組函數：①y=x²；②y=2^x；③y=log₂x；④y=2x哪個函數增長速度最快
（填序號）

17．從1到9這9個數字中取3個偶數和4個奇數，組成沒有重復數字的七位數，試問：
（1）能組成多少個這樣的七位數？
（2）3個偶數排在一起的七位數有多少個？
（3）任意2個偶數都不相鄰的七位數有多少個？

20．已知f（x）=e^x-1-a（x-1）．
（1）討論函數f（x）的單調性；
（2）若f（x）＞xlnx+ln
e
2
恒成立，求實數a的取值范圍．

21．已知函數f（x）=-
1
2
x
2
+ax-lnx（a∈R）．
（1）當a=1時，求曲線y=f（x）在點（1，f（1））處的切線方程；
（2）求f（x）的單調區間；
（3）若函數f（x）有兩個極值點x₁，x₂（x₁＜x₂），求證：4f（x₁）-2f（x₂）≤1+3ln2．

22．已知（
3
x
2
+3x）ⁿ展開式各項系數和比它的二項式系數和大992．
（1）求展開式中含有x⁴的項；
（2）求展開式中二項式系數最大的項；
（3）求展開式中系數最大的項．