2024年浙江省強基聯盟高考數學聯考試卷（3月份）

一、單項選擇題：本大題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.

• 1．若復數z₁對應復平面內的點（2，3），且z₁?z₂=1+i,則復數z₂的虛部為（　　）

  A． - 5 13

  B． 5 13

  C． - 1 13

  D． 1 13
  組卷：49引用：4難度：0.8

  解析

• 2．若函數f（x）對?x,y∈R，有f（x-y）=f（x）?f（y）+f（1+x）?f（1+y），且f（2）=-1，f（0）＞0，則f（2023）=（　　）

  A．0

  B．1

  C．-2022

  D．2022
  組卷：97引用：1難度：0.5

  解析

• 3．從5名同學中選若干名分別到圖書館、食堂做志愿者，若每個地方至少去2名，則不同的安排方法共有（　　）

  A．20種

  B．50種

  C．80種

  D．100種
  組卷：979引用：4難度：0.8

  解析

• 4．（x+2y）（x-y）⁵的展開式中x²y⁴的系數為（　　）

  A．-15

  B．5

  C．-20

  D．25
  組卷：619引用：5難度：0.8

  解析

• 5．已知集合A={x|x²-x-2＜0}，B=Z，則A∩B=（　　）

  A．{-1，0，1，2}

  B．{0，1，2}

  C．{0，1}

  D．{1}
  組卷：680引用：3難度：0.9

  解析

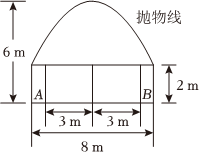• 6．如圖，一隧道內設雙行線公路，其截面由一個長方形和拋物線構成．為保證安全，要求行駛車輛頂部（設為平頂）與隧道頂部在豎直方向上高度之差至少要有0.5m,已知行車道總寬度|AB|=6m,那么車輛通過隧道的限制高度約為（　　）

  A．3.1m

  B．3.3m

  C．3.5m

  D．3.7m
  組卷：63引用：4難度：0.9

  解析

• 7．設a,b∈R，則“a+b＞9”是“a＞5且b＞4”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充分必要條件	D．既不充分又不必要條件
  組卷：74引用：4難度：0.9

  解析

• 8．17世紀，在研究天文學的過程中，為了簡化大數運算，蘇格蘭數學家納皮爾發明了對數，對數的思想方法即把乘方和乘法運算分別轉化為乘法和加法運算，數學家拉普拉斯稱贊“對數的發明在實效上等于把天文學家的壽命延長了許多倍”．已知lg2≈0.3010，lg3≈0.4771，設N=4⁵×9¹⁰，則N所在的區間為（　　）

  A．（1010，1011）	B．（1011，1012）
  C．（1012，1013）	D．（1013，1014）
  組卷：303引用：6難度：0.7

  解析

二、多項選擇題：本大題共3小題，每小題6分，共18分.在每小題給出的選項中，有多項符合題目要求.全部選對的得6分，部分選對的得部分分，有選錯的得0分.

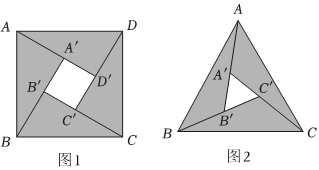• 9．東漢末年的數學家趙爽在《周髀算經》中利用一幅“弦圖”，根據面積關系給出了勾股定理的證明，后人稱其為“趙爽弦圖”，如圖1，它由四個全等的直角三角形與一個小正方形拼成的一個大正方形．某數學興趣小組通過類比得到圖2，它是由三個全等的鈍角三角形與一個小等邊三角形A′B′C′拼成的一個大等邊三角形ABC，對于圖2，下列結論正確的是（　　）

  A．這三個全等的鈍角三角形可能是等腰三角形

  B．若BB′=B′C′，則 BA 與 CA ′ 夾角的余弦值為 7 14

  C．若BB′=2B′C′，則△ABC的面積是△A′B′C′面積的19倍

  D．若BB′=2，B′C′=4，則△BCC′內切圓的半徑為 4 3 - 39
  組卷：18引用：1難度：0.4

  解析

• 10．有兩組樣本數據，分別為x₁，x₂ …x₆和y₁，y₂，y₃，y₄，且平均數

  x

  =90與

  y

  =80，標準差分別為6和4，將兩組數據合并為z₁，z₂ …，z₁₀，重新計算平均數和標準差，則（　　）

  A．平均數為85	B．平均數為86
  C．標準差為10	D．標準差為 2 13
  組卷：70引用：6難度：0.7

  解析

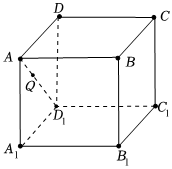• 11．如圖，在正方體ABCD-A₁B₁C₁D₁中，點Q在線段AD₁上運動（包括端點），則（　　）

  A．直線CQ與直線B1D互相垂直

  B．直線CQ與直線B1D是異面直線

  C．存在點Q使得直線CQ與直線A1C1所成的角為45°

  D．當Q是線段AD1的中點時，二面角Q-B1C1-A1的平面角的余弦值為 2 5 5
  組卷：171引用：1難度：0.5

  解析

三、填空題：本大題共3小題，每小題5分，共15分.

• 12．已知平面向量

  a

  =

  （

  1

  ，

  2

  ）

  ，

  b

  =

  （

  -

  1

  ，

  1

  ）

  ，若

  k

  a

  +

  b

  與

  a

  -

  3

  b

  垂直，則實數k=

  ．
  組卷：23引用：2難度：0.8

  解析

• 13．若對于圓C：x²+y²-2x-2y-2=0上任意的點A，直線l：4x+3y+8=0上總存在不同兩點M，N，使得∠MAN≥90°，則|MN|的最小值為

  ．
  組卷：221引用：4難度：0.5

  解析

• 14．已知數列{a_n}的前n項和S_n=2ⁿ+1，則a_n=

  ．
  組卷：11引用：2難度：0.7

  解析

四、解答題：本大題共5小題，共77分.解答應寫出文字說明、證明過程或演算步驟.

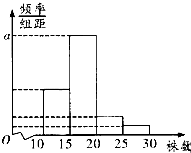• 15．某單位組織職工開展構建綠色家園活動，在今年3月份參加義務植樹活動的職工中，隨機抽取M名職工為樣本，得到這些職工植樹的株數，根據此數據作出了頻數與頻率統計表和頻率分布直方圖如圖：
  （1）求出表中M，p及圖中a的值；
  （2）單位決定對參加植樹的職工進行表彰，對植樹株數在[25，30）區間的職工發放價值800元的獎品，對植樹株數在[20，25）區間的職工發放價值600元的獎品，對植樹株數在[15，20）區間的職工發放價值400元的獎品，對植樹株數在[10，15）區間的職工發放價值200元的獎品，在所取樣本中，任意取出2人，并設X為此二人所獲得獎品價值之差的絕對值，求X的分布列與數學期望E（X）．
  

  分組	頻數	頻率
  [10，15）	5	0.25
  [15，20）	12	n
  [20，25）	m	p
  [25，30）	1	0.05
  合計	M	1
  組卷：89引用：2難度：0.5

  解析

• 16．某地為了慶祝國慶66周年，現計劃在城市中心廣場搭建一個巨型花籃（如圖甲）．其中主體框梨（如圖乙）準備用鋼材焊接而成，具體設計方案如下：①上、中、下三部分依次由正六棱臺、正六棱柱、正六棱臺組成；②這三個幾何體的側面用于張貼宣傳城市風光的圖片，且側面積之和為108m²；③BC：B₁C₁：B₃C₃=1：2：4，∠BB₁C₁=∠B₂B₃C₃=α，且sinα=

  4

  5

  ，設BC=xm,B₁B₂=ym.
  （1）試將y表示為x的函數，并求函數的定義域；
  （2）當x為多少時，焊接主體框架的鋼材用料最省？
  組卷：6引用：0難度：0.9

  解析

• 17．已知函數f（x）=e^x-x-1．
  （1）求證：f（x）≥0；
  （2）若xe^2x≥lnx+ax+1恒成立，求實數a的取值范圍．
  組卷：34引用：1難度：0.3

  解析

• 18．已知橢圓E：

  x

  2

  4

  +

  y

  2

  3

  =1的兩個焦點分別為F₁、F₂，直線l：y=kx+m（k,m∈R）與橢圓交于A、B兩點．
  （1）若直線l經過點C（0，3），且|OA|=|AC|，求點A的坐標；
  （2）若直線l經過點C（0，3），且S_△AOC=S_△AOB，求直線l的方程．
  （3）若k_OA?k_OB=-

  3

  4

  ，則△AOB的面積是否為定值？如果是，求出該定值；如果不是，請說明理由．
  組卷：92引用：1難度：0.5

  解析

• 19．已知cosα=

  5

  5

  ，sin（α-β）=

  10

  10

  ，且α，β∈（0，

  π

  2

  ）．求：
  （1）cos（α-β）的值；
  （2）β的值．
  組卷：347引用：7難度：0.6

  解析