當前位置：試卷中心 > 試卷詳情

2023-2024學年湖南省株洲市炎陵縣高二（上）入學數(shù)學試卷

發(fā)布：2025/6/29 2:0:12

一、選擇題：本題共8小題，每小題5分，共40分．在每小題的四個選項中，只有一項是符合題目要求的．

1．兩個圓錐的底面是一個球的同一截面，頂點均在球面上，若球的半徑為2，兩個圓錐的高之比為1：3，則這兩個圓錐的體積之和為（　　）
A．3π B．4π C．9π D．12π
組卷：8引用：1難度：0.6
解析
2．已知
a
，
b
是不共線的向量，且
AB
=
3
a
+
4
b
，
BC
=
-
2
a
-
6
b
，
CD
=
2
a
-
4
b
，則（　　）
A．A、B、D三點共線 B．A、B、C三點共線
C．B、C、D三點共線 D．A、C、D三點共線
組卷：251引用：2難度：0.7
解析
3．2023年3月1日，“中國日報視覺”學習強國號上線．某黨支部理論學習小組抽取了10位黨員在該學習平臺的學習成績?nèi)缦拢?3，85，88，90，91，91，92，93，96，97，則這10名黨員學習成績的75%分位數(shù)為（　　）
A．90 B．92 C．93 D．92.5
組卷：41引用：2難度：0.8
解析
4．已知兩條直線l,m和一個平面α，下列說法正確的是（　　）
A．若l⊥m,m∥α，則l⊥α B．若l⊥m,l⊥α，則m∥α
C．若l⊥α，m∥α，則l⊥m D．若l∥α，m∥α，則l∥m
組卷：332引用：4難度：0.6
解析
5．復數(shù)
1
+
i
i
3
（i是虛數(shù)單位）在復平面上對應(yīng)的點位于（　　）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
組卷：65引用：7難度：0.9
解析
6．設(shè)復數(shù)z滿足1+i?z=2i,則z=（　　）
A．2-i B．2+i C．1-2i D．1+2i
組卷：16引用：1難度：0.8
解析
7．樣本數(shù)據(jù)x₁，x₂，…，x_n的平均數(shù)
x
=
4
，方差S²=1，則樣本數(shù)據(jù)2x₁+1，2x₂+1，…，2x_n+1的平均數(shù)，方差分別為（　　）
A．9，4 B．9，2 C．4，1 D．2，1
組卷：281引用：11難度：0.8
解析
8．已知四棱錐S-ABCD，底面ABCD為矩形，AB=2BC=2，平面SAD⊥平面ABCD，△SAD為正三角形．則四棱錐S-ABCD的外接球的體積為（　　）
A．
32
3
27
π
B．
16
3
27
π
C．
32
3
9
π
D．
16
3
9
π
組卷：235引用：1難度：0.5
解析

二、多項選擇題：本題共4小題，每小題滿分20分，共20分．在每小題給出的四個選項中，有多項符合題目要求．全部選對得5分，部分選對得2分，有選錯的得0分．

9．下列命題為假命題的是（　　）

A．?x₀∈R，x₀²+4x₀+6≤0

B．正切函數(shù)y=tanx的定義域為R

C．函數(shù)

的單調(diào)遞減區(qū)間為（-∞，0）∪（0，+∞）

D．矩形的對角線相等且互相平分

組卷：6引用：1難度：0.5

解析

10．目前，我國老年人口比例不斷上升，造成日趨嚴峻的人口老齡化問題.2019年10月12日，北京市老齡辦、市老齡協(xié)會聯(lián)合北京師范大學中國公益研究院發(fā)布《北京市老齡事業(yè)發(fā)展報告（2018）》，相關(guān)數(shù)據(jù)有如圖．下列說法中正確的是（　　）

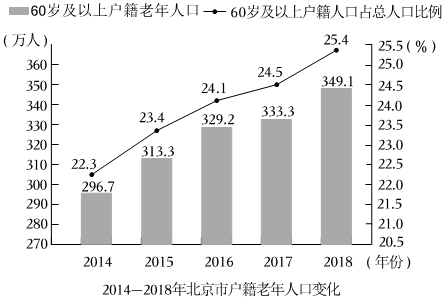
A．2014年以來，60歲及以上戶籍人口比例的增長速度逐年上升

B．2014年至2018年，60歲及以上戶籍人口比例逐年增加

C．2014年至2018年，60歲及以上戶籍老年人口的30%分位數(shù)為313.3萬人

D．估算北京市2018年戶籍總?cè)丝跀?shù)約為1374萬人

組卷：49引用：1難度：0.5

解析

11．在△ABC中，
AD
=
3
4
AB
+
1
4
AC
，BC=4，tan∠ADC=
2
3
，|
AD
|
=
13
．則下列結(jié)論正確的有（　　）
A．BD=3DC B．AC=2
C．△ABC的面積為3 D．△ABC的外接圓半徑為
5
組卷：145引用：1難度：0.5
解析
12．已知正方體ABCD-A₁B₁C₁D₁的棱長為1，點P是線段BD₁上（不含端點）的任意一點，點E是線段A₁B的中點，點F是平面ABCD內(nèi)一點，則下面結(jié)論中正確的有（　　）
A．CD∥平面PBC₁
B．以A₁為球心、
2
為半徑的球面與該正方體側(cè)面DCC₁D₁的交線長是
π
2
C．|EP|+|PF|的最小值是
2
3
D．|EP|+|PF|的最小值是
2
3
組卷：203引用：2難度：0.5
解析

三、填空題：本題共4小題，每小題5分，共20分．

13．已知復數(shù)
z
=
1
-
2
i
i
（i是虛數(shù)單位），則z的虛部是
．
組卷：35引用：1難度：0.8
解析
14．甲、乙兩人輪流投籃，每人每次投一球．約定甲先投且先投中者獲勝，一直到有人獲勝或每人都已投球3次時投籃結(jié)束．設(shè)甲每次投籃投中的概率為
1
4
，乙每次投籃投中的概率為
1
3
，且各次投籃互不影響．則乙獲勝的概率為
；投籃結(jié)束時，乙只投了2個球的概率為
．
組卷：6引用：0難度：0.7
解析
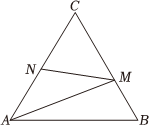15．如圖，在等邊三角形ABC中，AB=2，點N為AC的中點，點M是邊CB（包括端點）上的一個動點，則
AM
?
NM
的最小值為
．
組卷：105引用：2難度：0.5
解析
16．某個年級有男生560人，女生420人，用分層抽樣的方法從該年級全體學生中抽取一個容量為280的樣本，則此樣本中男生人數(shù)為
．
組卷：534引用：32難度：0.7
解析

四、解答題：本題共6小題，共70分．解答應(yīng)寫出文字說明、證明過程或演算步驟．

17．記△ABC的內(nèi)角A，B，C所對的邊分別為a,b,c,已知
bsin
C
=
sin
C
+
3
cos
C
，
A
=
π
3
．
（1）求c；
（2）在下列三個條件中選擇一個作為補充條件，判斷該三角形是否存在？若存在，求出三角形的面積；若不存在，說明理由．
①BC邊上的中線長為
2
2
；
②AB邊上的中線長為
7
；
③三角形的周長為6．
組卷：268引用：3難度：0.6
解析
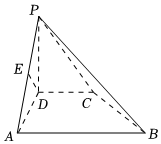18．在四棱錐P-ABCD中，PD⊥平面ABCD，AB∥DC，AB⊥AD，
CD
=
AD
=
1
2
AB
，∠PAD=45°，E是PA的中點，G在線段AB上，且滿足CG⊥BD．
（1）求證：DE∥平面PBC；
（2）求平面PGC與平面BPC夾角的余弦值；
（3）在線段PA上是否存在點H，使得GH與平面PGC所成角的正弦值是
3
3
，若存在，求出AH的長；若不存在，請說明理由．
組卷：333引用：10難度：0.5
解析
19．多項選擇題是高考的一種題型，其規(guī)則如下：有多項符合題目要求，全部選對的得5分，有選錯的得0分，部分選對的得2分．現(xiàn)高二某同學正在進行第一次月考，做到多項選擇題的11題和12題．該同學發(fā)現(xiàn)自己只能全憑運氣，在這兩個多項選擇題中，他選擇一個選項的概率是
1
2
，選擇兩個選項的概率是
1
3
，選擇三個選項的概率是
1
6
．已知該同學做題時題目與題目之間互不影響且第11題正確答案是兩個選項，第12題正確答案是三個選項．
（1）求該同學11題得5分的概率；
（2）求該同學兩個題總共得分不小于7分的概率．
組卷：163引用：4難度：0.8
解析
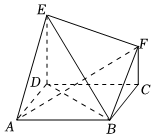20．如圖，在多面體ABCDEF中，ABCD為正方形，DE⊥平面ABCD，CF∥DE，DE=DC=2CF=2．
（Ⅰ）求證：BF∥平面ADE；
（Ⅱ）求直線BD與平面AEF所成角的大小．
組卷：196引用：5難度：0.5
解析
21．某校為了解高三年級1000名學生對“高中語文必背篇目”的掌握情況，舉行了一次“古詩文”測試．現(xiàn)隨機抽取100名學生，對其測試成績（滿分：100分）進行統(tǒng)計，得到樣本的頻率分布直方圖，如圖所示．若測試成績低于平均分，則視為“不合格”，若測試成績排名進入前15%，則可獲得“優(yōu)秀獎”．
?（1）請根據(jù)樣本數(shù)據(jù)，估計全年級的平均分和獲得“優(yōu)秀獎”的劃線成績；
（2）甲、乙、丙三位同學因測試結(jié)果不理想，組成互助學習小組，通過挑戰(zhàn)游戲的方式加強練習，挑戰(zhàn)游戲規(guī)則如下：游戲共有3輪，每輪由一位同學出一道“背誦”或“默寫”題，另外兩位同學同時獨立答題，若兩位同學都答對或兩位同學都答錯，原出題的同學繼續(xù)出題，游戲進入下一輪；若兩位同學中僅有一位同學答對，則答對的同學出下一道題，另兩位同學作答，游戲進入下一輪．每答對一道“默寫”題得10分，每答對一道“背誦”題得5分，答錯和出題均不得分，第一輪由甲開始出題．
現(xiàn)已知出題時，甲、乙、丙出“默寫”題的概率分別為
1
2
，
1
3
，
1
4
，當答題時，甲、乙、丙答對“背誦”題和“默寫”題的概率如下表所示：

甲乙丙

背誦
1
2

2
3

1
3

默寫
1
2

1
3

2
3

①求第一輪結(jié)束時，乙的得分X的分布列和期望；
②求第三輪仍由甲出題的概率．
組卷：211引用：1難度：0.3
解析
22．已知函數(shù)f（x）=
3
sinωxcosωx-cos²ωx+m.
（1）若f（x）的圖象關(guān)于直線x=
2
π
9
對稱，ω∈[1，π]，求f（x）的單調(diào)遞增區(qū)間；
（2）在（1）的條件下，當x∈[0，
π
2
]時，x₁和x₂是f（x）的兩個零點，求f（x₁+x₂）-m的值和m的取值范圍．
組卷：146引用：4難度：0.5
解析

0/60 進入組卷

0/20 進入試卷籃

布置作業(yè) 發(fā)布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

A．A、B、D三點共線	B．A、B、C三點共線
C．B、C、D三點共線	D．A、C、D三點共線

A．若l⊥m,m∥α，則l⊥α	B．若l⊥m,l⊥α，則m∥α
C．若l⊥α，m∥α，則l⊥m	D．若l∥α，m∥α，則l∥m

A．BD=3DC	B．AC=2
C．△ABC的面積為3	D．△ABC的外接圓半徑為 5

	甲	乙	丙
背誦	1 2	2 3	1 3
默寫	1 2	1 3	2 3

2023-2024學年湖南省株洲市炎陵縣高二（上）入學數(shù)學試卷

一、選擇題：本題共8小題，每小題5分，共40分．在每小題的四個選項中，只有一項是符合題目要求的．

1．兩個圓錐的底面是一個球的同一截面，頂點均在球面上，若球的半徑為2，兩個圓錐的高之比為1：3，則這兩個圓錐的體積之和為（ ）

2．已知a，b是不共線的向量，且AB=3a+4b，BC=-2a-6b，CD=2a-4b，則（ ）

3．2023年3月1日，“中國日報視覺”學習強國號上線．某黨支部理論學習小組抽取了10位黨員在該學習平臺的學習成績?nèi)缦拢?3，85，88，90，91，91，92，93，96，97，則這10名黨員學習成績的75%分位數(shù)為（ ）

4．已知兩條直線l,m和一個平面α，下列說法正確的是（ ）

5．復數(shù)1+ii3（i是虛數(shù)單位）在復平面上對應(yīng)的點位于（ ）

6．設(shè)復數(shù)z滿足1+i?z=2i,則z=（ ）

7．樣本數(shù)據(jù)x1，x2，…，xn的平均數(shù)x=4，方差S2=1，則樣本數(shù)據(jù)2x1+1，2x2+1，…，2xn+1的平均數(shù)，方差分別為（ ）

8．已知四棱錐S-ABCD，底面ABCD為矩形，AB=2BC=2，平面SAD⊥平面ABCD，△SAD為正三角形．則四棱錐S-ABCD的外接球的體積為（ ）

二、多項選擇題：本題共4小題，每小題滿分20分，共20分．在每小題給出的四個選項中，有多項符合題目要求．全部選對得5分，部分選對得2分，有選錯的得0分．

9．下列命題為假命題的是（ ）

11．在△ABC中，AD=34AB+14AC，BC=4，tan∠ADC=23，|AD|=13．則下列結(jié)論正確的有（ ）

12．已知正方體ABCD-A1B1C1D1的棱長為1，點P是線段BD1上（不含端點）的任意一點，點E是線段A1B的中點，點F是平面ABCD內(nèi)一點，則下面結(jié)論中正確的有（ ）

三、填空題：本題共4小題，每小題5分，共20分．

13．已知復數(shù)z=1-2ii（i是虛數(shù)單位），則z的虛部是 ．

15．如圖，在等邊三角形ABC中，AB=2，點N為AC的中點，點M是邊CB（包括端點）上的一個動點，則AM?NM的最小值為 ．

16．某個年級有男生560人，女生420人，用分層抽樣的方法從該年級全體學生中抽取一個容量為280的樣本，則此樣本中男生人數(shù)為．

四、解答題：本題共6小題，共70分．解答應(yīng)寫出文字說明、證明過程或演算步驟．

20．如圖，在多面體ABCDEF中，ABCD為正方形，DE⊥平面ABCD，CF∥DE，DE=DC=2CF=2．（Ⅰ）求證：BF∥平面ADE；（Ⅱ）求直線BD與平面AEF所成角的大小．

1．兩個圓錐的底面是一個球的同一截面，頂點均在球面上，若球的半徑為2，兩個圓錐的高之比為1：3，則這兩個圓錐的體積之和為（　　）

2．已知
a
，
b
是不共線的向量，且
AB
=
3
a
+
4
b
，
BC
=
-
2
a
-
6
b
，
CD
=
2
a
-
4
b
，則（　　）

3．2023年3月1日，“中國日報視覺”學習強國號上線．某黨支部理論學習小組抽取了10位黨員在該學習平臺的學習成績?nèi)缦拢?3，85，88，90，91，91，92，93，96，97，則這10名黨員學習成績的75%分位數(shù)為（　　）

4．已知兩條直線l,m和一個平面α，下列說法正確的是（　　）

5．復數(shù)
1
+
i
i
3
（i是虛數(shù)單位）在復平面上對應(yīng)的點位于（　　）

6．設(shè)復數(shù)z滿足1+i?z=2i,則z=（　　）

7．樣本數(shù)據(jù)x₁，x₂，…，x_n的平均數(shù)
x
=
4
，方差S²=1，則樣本數(shù)據(jù)2x₁+1，2x₂+1，…，2x_n+1的平均數(shù)，方差分別為（　　）

8．已知四棱錐S-ABCD，底面ABCD為矩形，AB=2BC=2，平面SAD⊥平面ABCD，△SAD為正三角形．則四棱錐S-ABCD的外接球的體積為（　　）

9．下列命題為假命題的是（　　）

11．在△ABC中，
AD
=
3
4
AB
+
1
4
AC
，BC=4，tan∠ADC=
2
3
，|
AD
|
=
13
．則下列結(jié)論正確的有（　　）

12．已知正方體ABCD-A₁B₁C₁D₁的棱長為1，點P是線段BD₁上（不含端點）的任意一點，點E是線段A₁B的中點，點F是平面ABCD內(nèi)一點，則下面結(jié)論中正確的有（　　）

13．已知復數(shù)
z
=
1
-
2
i
i
（i是虛數(shù)單位），則z的虛部是
．

15．如圖，在等邊三角形ABC中，AB=2，點N為AC的中點，點M是邊CB（包括端點）上的一個動點，則
AM
?
NM
的最小值為
．

16．某個年級有男生560人，女生420人，用分層抽樣的方法從該年級全體學生中抽取一個容量為280的樣本，則此樣本中男生人數(shù)為
．

20．如圖，在多面體ABCDEF中，ABCD為正方形，DE⊥平面ABCD，CF∥DE，DE=DC=2CF=2．
（Ⅰ）求證：BF∥平面ADE；
（Ⅱ）求直線BD與平面AEF所成角的大小．