當前位置：試卷中心 > 試卷詳情

2021年東北三省四市教研聯合體高考數學模擬試卷（理科）（二）（4月份）

發布：2025/6/29 3:0:17

一、選擇題：本題共12小題，每小題5分，在每小題給出的四個選項中，只有一項是符合題目要求的.

1．已知集合A={-1，1，2}，B={x|x²=x}，則A∩B=（　　）
A．{-1} B．{1} C．{-1，1} D．{-1，0，1，2}
組卷：110引用：6難度：0.8
解析
2．若復數z滿足i?z=z+2-i,則|z-i|=（　　）
A．
2
B．
3
2
2
C．
5
2
2
D．6
組卷：23引用：1難度：0.8
解析
3．已知數列{a_n}的前n項和
S
n
=
n
2
-
7
n
，若3＜a_k＜5，則k=（　　）
A．8 B．7 C．6 D．5
組卷：491引用：6難度：0.7
解析
4．在一個文藝比賽中，8名專業人士和12名觀眾代表各組成一個評委小組，給參賽選手打分，根據打分情況，得到專業人士組對選手A打分的平均數為48，方差為14，觀眾代表組對選手A打分的平均數為56，方差為140，則選手A得分的總方差為（　　）
A．105.60 B．85.24 C．94.63 D．104.96
組卷：61引用：2難度：0.7
解析
5．已知函數
f
（
x
）
=
sinωx
-
cos
（
ωx
+
π
6
）
（
ω
＞
0
）
在[0，π]上有且僅有2個零點，則ω的取值范圍是（　　）
A．
[
1
，
13
6
]
B．
[
7
6
，
13
6
）
C．
[
7
6
，
2
）
D．
[
1
，
13
6
）
組卷：497引用：4難度：0.6
解析
6．已知橢圓的標準方程為
x
2
9
+
y
2
10
=1，則橢圓的焦點坐標為（　　）
A．（1，0），（-1，0） B．（0，1），（0，-1）
C．（
19
，0），（-
19
，0） D．（0，
19
），（0，-
19
）
組卷：149引用：1難度：0.8
解析
7．若a＞0，b＞0，則“ab≤4”是“a+b≤4”的（　　）
A．充分不必要條件 B．充要條件
C．必要不充分條件 D．既不充分又不必要
組卷：531引用：4難度：0.7
解析
8．已知函數f（x）=2sin（
π
4
-3x）+1，則函數的最小正周期為（　　）
A．8 B．2π C．π D．
2
π
3
組卷：238引用：3難度：0.8
解析
9．下列結論正確的是（　　）
A．若a＞b,c＞b,則a＞c B．若a＞b,則a²＞b²
C．若a＞b,c＞d,則ac＞bd D．若a＞b,c＞d,則a+c＞b+d
組卷：141引用：10難度：0.9
解析
10．已知向量
a
=（sinx,cosx），向量
b
=
（
1
，
3
）
，則|
a
+
b
|的最大值為（　　）
A．3 B．
3
C．1 D．9
組卷：460引用：13難度：0.9
解析
11．編號為1，2，3，4，5的五位同學分別就座于編號為1，2，3，4，5的五個座位上，每位座位恰好坐一位同學，則恰有兩位同學的編號和座位編號一致的坐法種數為（　　）
A．20 B．45 C．40 D．90
組卷：62引用：1難度：0.8
解析
12．已知函數f（x）=mx+1的零點在區間（1，2）內，則m的取值范圍是（　　）
A．
（
-
∞
，-
1
2
）
B．
（
-
1
，-
1
2
）
C．（-
1
2
，+∞） D．
（
-
∞
，-
1
）
∪
（
-
1
2
，
+
∞
）
組卷：361引用：3難度：0.8
解析

二、填空題：本題共4小題，每小題5分.

13．（1+ax）⁵的展開式各項系數的和是-1，則a=
．
組卷：92引用：7難度：0.8
解析
14．如圖（1），畫一個邊長為1的正三角形，并把每一邊三等分，在每個邊上以中間一段為一邊，向外側凸出作正三角形，再把原來邊上中間一段擦掉，得到第（2）個圖形，重復上面的步驟，得到第（3）個圖形，這樣無限地作下去，得到的圖形的輪廓線稱為科赫曲線．云層的邊緣、山脈的輪廓、海岸線等自然界里的不規則曲線都可用“科赫曲線”的方式來研究，這門學科叫“分形幾何學”．

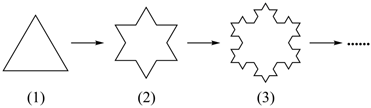
設第（n）個圖形的周長為a_n，則a_n+1與a_n的遞推關系式為
，當a_n≥10a₁時，n的最小值為
（參考數據：lg4≈0.60，lg3≈0.48）
組卷：18引用：1難度：0.6
解析
15．已知F₁，F₂為雙曲線
x
2
a
2
-
y
2
b
2
=
1
（
a
＞
0
，
b
＞
0
）
的兩個焦點，過點F₂且垂直于x軸的直線交雙曲線于點P，且∠F₁PF₂=60°，則此雙曲線的漸近線方程為
．
組卷：115引用：1難度：0.6
解析
16．設△ABC的內角A，B，C所對的邊分別為a,b,c,且a+c=6，
b
=
2
，
cos
B
=
7
9
，則△ABC的面積S=
．
組卷：35引用：2難度：0.6
解析

三、解答題：共70分，解答應寫出文字說明、證明過程或演算步驟。第17～21題為必考題，每個試題考生都必須作答。第22～23題為選考題，考生根據要求作答.（一）必考題：共60分.

17．已知bg糖水中有ag糖（b＞a＞0），往糖水中加入mg糖（m＞0），（假設全部溶解）糖水更甜了．
（1）請將這個事實表示為一個不等式；
（2）證明這個不等式；
（3）利用（1）的結論證明命題：“若在△ABC中a、b、c分別為角A、B、C所對的邊長，則
c
1
+
c
＜
a
1
+
a
+
b
1
+
b
”．
組卷：51引用：3難度：0.8
解析
18．在直角坐標系xOy中，曲線C的參數方程為
x
=
sint
y
=
cost
（t為參數）．以坐標原點O為極點，x的正半軸為極軸建立極坐標系，直線l的極坐標方程為
2
sinθ
-
15
cosθ
=
0
．
（1）求曲線C的普通方程；
（2）若P是曲線C上一動點，求|PO|的最大值；
（3）求直線l與曲線C交點的直角坐標．
組卷：29引用：2難度：0.5
解析
19．已知函數f（x）=lnx-ae^x+1（a∈R）．
（1）當a=1時，討論f（x）極值點的個數；
（2）若函數f（x）有兩個零點，求a的取值范圍．
組卷：382引用：6難度：0.5
解析

20．第17屆亞運會將于2014年9月18日至10月4日在韓國仁川進行，為了搞好接待工作，組委會招募了16名男志愿者和14名女志愿者，調查發現，男、女志愿者中分別有10人和6人喜愛運動，其余不喜愛．
（1）根據調查數據制作2×2列聯表；
（2）根據列聯表的獨立性檢驗，能否認為性別與喜愛運動有關？

參考數據當Χ²≤2.706時，無充分證據判定變量A，B有關聯，可以認為兩變量無關聯；

當Χ²＞2.706時，有90%把握判定變量A，B有關聯；

當Χ²＞3.841時，有95%把握判定變量A，B有關聯；

當Χ²＞6.635時，有99%把握判定變量A，B有關聯．

（參考公式：
Χ
2
=
n
（
ad
-
bc
）
2
（
a
+
b
）
（
c
+
d
）
（
a
+
c
）
（
b
+
d
）
，其中n=a+b+c+d.）

組卷：10引用：3難度：0.5

解析

21．設S_n為數列{a_n}的前n項和，對任意的n∈N^*，都有S_n=（m+1）-ma_n（m為常數，且m＞0）．
（1）求證：數列{a_n}是等比數列．
（2）設數列{a_n}的公比q=f（m），數列{b_n}滿足b₁=2a₁，b_n=f（b_n-1）（n≥2，n∈N^*），求數列{b_n}的通項公式．
（3）在滿足（2）的條件下，求數列
{
2
n
+
1
b
n
}
的前n項和T_n
組卷：340引用：16難度：0.5
解析

（二）選考題：共10分，請考生在22、23題中任選一題作答，如果多做則按所做的第一題計分.[選修4-4坐標系與參數方程]

22．已知橢圓的焦點坐標是F₁（-1，0），F₂（1，0），M是橢圓上一點，且
|
M
F
1
|
+
|
M
F
2
|
=
2
5
．
（1）求此橢圓的標準方程；
（2）若直線y=x+m交橢圓于A，B兩點，且AB的中點為P（-1，n），求n的值．
組卷：2引用：0難度：0.5
解析

[選修4-5不等式選講]

23．已知空間幾何體ABCDEF，底面ABCD為菱形，∠DAB=60°，EF∥AB，AE=DE，AB=2，EF=1，平面ADE⊥平面ABCD，
BM
=
1
3
BF
，
AN
=
1
2
AD
．
（1）求證：EN⊥BC；
（2）若直線AE與平面ABCD所成角為60°，求直線AM與平面BCF所成角的正弦值．
組卷：65引用：1難度：0.5
解析

0/60 進入組卷

0/20 進入試卷籃

布置作業 發布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

A．（1，0），（-1，0）	B．（0，1），（0，-1）
C．（ 19 ，0），（- 19 ，0）	D．（0， 19 ），（0，- 19 ）

A．充分不必要條件	B．充要條件
C．必要不充分條件	D．既不充分又不必要

A．若a＞b,c＞b,則a＞c	B．若a＞b,則a²＞b²
C．若a＞b,c＞d,則ac＞bd	D．若a＞b,c＞d,則a+c＞b+d

A．（ - ∞ ，- 1 2 ）	B．（ - 1 ，- 1 2 ）
C．（- 1 2 ，+∞）	D．（ - ∞ ，- 1 ） ∪ （ - 1 2 ， + ∞ ）

參考數據	當Χ²≤2.706時，無充分證據判定變量A，B有關聯，可以認為兩變量無關聯；
	當Χ²＞2.706時，有90%把握判定變量A，B有關聯；
	當Χ²＞3.841時，有95%把握判定變量A，B有關聯；
	當Χ²＞6.635時，有99%把握判定變量A，B有關聯．

2021年東北三省四市教研聯合體高考數學模擬試卷（理科）（二）（4月份）

一、選擇題：本題共12小題，每小題5分，在每小題給出的四個選項中，只有一項是符合題目要求的.

1．已知集合A={-1，1，2}，B={x|x2=x}，則A∩B=（ ）

2．若復數z滿足i?z=z+2-i,則|z-i|=（ ）

3．已知數列{an}的前n項和Sn=n2-7n，若3＜ak＜5，則k=（ ）

5．已知函數f（x）=sinωx-cos（ωx+π6）（ω＞0）在[0，π]上有且僅有2個零點，則ω的取值范圍是（ ）

6．已知橢圓的標準方程為x29+y210=1，則橢圓的焦點坐標為（ ）

7．若a＞0，b＞0，則“ab≤4”是“a+b≤4”的（ ）

8．已知函數f（x）=2sin（π4-3x）+1，則函數的最小正周期為（ ）

9．下列結論正確的是（ ）

10．已知向量a=（sinx,cosx），向量b=（1，3），則|a+b|的最大值為（ ）

11．編號為1，2，3，4，5的五位同學分別就座于編號為1，2，3，4，5的五個座位上，每位座位恰好坐一位同學，則恰有兩位同學的編號和座位編號一致的坐法種數為（ ）

12．已知函數f（x）=mx+1的零點在區間（1，2）內，則m的取值范圍是（ ）

二、填空題：本題共4小題，每小題5分.

13．（1+ax）5的展開式各項系數的和是-1，則a=．

15．已知F1，F2為雙曲線x2a2-y2b2=1（a＞0，b＞0）的兩個焦點，過點F2且垂直于x軸的直線交雙曲線于點P，且∠F1PF2=60°，則此雙曲線的漸近線方程為 ．

16．設△ABC的內角A，B，C所對的邊分別為a,b,c,且a+c=6，b=2，cosB=79，則△ABC的面積S=．

三、解答題：共70分，解答應寫出文字說明、證明過程或演算步驟。第17～21題為必考題，每個試題考生都必須作答。第22～23題為選考題，考生根據要求作答.（一）必考題：共60分.

19．已知函數f（x）=lnx-aex+1（a∈R）．（1）當a=1時，討論f（x）極值點的個數；（2）若函數f（x）有兩個零點，求a的取值范圍．

（二）選考題：共10分，請考生在22、23題中任選一題作答，如果多做則按所做的第一題計分.[選修4-4坐標系與參數方程]

22．已知橢圓的焦點坐標是F1（-1，0），F2（1，0），M是橢圓上一點，且|MF1|+|MF2|=25．（1）求此橢圓的標準方程；（2）若直線y=x+m交橢圓于A，B兩點，且AB的中點為P（-1，n），求n的值．

[選修4-5不等式選講]

23．已知空間幾何體ABCDEF，底面ABCD為菱形，∠DAB=60°，EF∥AB，AE=DE，AB=2，EF=1，平面ADE⊥平面ABCD，BM=13BF，AN=12AD．（1）求證：EN⊥BC；（2）若直線AE與平面ABCD所成角為60°，求直線AM與平面BCF所成角的正弦值．

1．已知集合A={-1，1，2}，B={x|x²=x}，則A∩B=（　　）

2．若復數z滿足i?z=z+2-i,則|z-i|=（　　）

3．已知數列{a_n}的前n項和
S
n
=
n
2
-
7
n
，若3＜a_k＜5，則k=（　　）

5．已知函數
f
（
x
）
=
sinωx
-
cos
（
ωx
+
π
6
）
（
ω
＞
0
）
在[0，π]上有且僅有2個零點，則ω的取值范圍是（　　）

6．已知橢圓的標準方程為
x
2
9
+
y
2
10
=1，則橢圓的焦點坐標為（　　）

7．若a＞0，b＞0，則“ab≤4”是“a+b≤4”的（　　）

8．已知函數f（x）=2sin（
π
4
-3x）+1，則函數的最小正周期為（　　）

9．下列結論正確的是（　　）

10．已知向量
a
=（sinx,cosx），向量
b
=
（
1
，
3
）
，則|
a
+
b
|的最大值為（　　）

11．編號為1，2，3，4，5的五位同學分別就座于編號為1，2，3，4，5的五個座位上，每位座位恰好坐一位同學，則恰有兩位同學的編號和座位編號一致的坐法種數為（　　）

12．已知函數f（x）=mx+1的零點在區間（1，2）內，則m的取值范圍是（　　）

13．（1+ax）⁵的展開式各項系數的和是-1，則a=
．

15．已知F₁，F₂為雙曲線
x
2
a
2
-
y
2
b
2
=
1
（
a
＞
0
，
b
＞
0
）
的兩個焦點，過點F₂且垂直于x軸的直線交雙曲線于點P，且∠F₁PF₂=60°，則此雙曲線的漸近線方程為
．

16．設△ABC的內角A，B，C所對的邊分別為a,b,c,且a+c=6，
b
=
2
，
cos
B
=
7
9
，則△ABC的面積S=
．

19．已知函數f（x）=lnx-ae^x+1（a∈R）．
（1）當a=1時，討論f（x）極值點的個數；
（2）若函數f（x）有兩個零點，求a的取值范圍．

22．已知橢圓的焦點坐標是F₁（-1，0），F₂（1，0），M是橢圓上一點，且
|
M
F
1
|
+
|
M
F
2
|
=
2
5
．
（1）求此橢圓的標準方程；
（2）若直線y=x+m交橢圓于A，B兩點，且AB的中點為P（-1，n），求n的值．

23．已知空間幾何體ABCDEF，底面ABCD為菱形，∠DAB=60°，EF∥AB，AE=DE，AB=2，EF=1，平面ADE⊥平面ABCD，
BM
=
1
3
BF
，
AN
=
1
2
AD
．
（1）求證：EN⊥BC；
（2）若直線AE與平面ABCD所成角為60°，求直線AM與平面BCF所成角的正弦值．