當(dāng)前位置：試卷中心 > 試卷詳情

2023年廣西名校高考數(shù)學(xué)聯(lián)考試卷（文科）（3月份）

發(fā)布：2025/6/29 4:0:12

一、選擇題：本題共12小題，每小題5分，共60分.在每小題給出的四個(gè)選項(xiàng)中，只有一項(xiàng)是符合題目要求的.

1．如果橢圓
x
2
k
+
8
+
y
2
9
=
1
（
k
＞
-
8
）
的離心率為e=
1
2
，則k=（　　）
A．4 B．4或
-
5
4
C．-
4
5
D．4或
-
4
5
組卷：555引用：6難度：0.7
解析
2．復(fù)數(shù)z滿足（1+i）z=i,則在復(fù)平面內(nèi)復(fù)數(shù)z所對(duì)應(yīng)的點(diǎn)位于（　　）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
組卷：133引用：12難度：0.9
解析
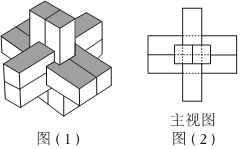3．榫卯，是一種中國傳統(tǒng)建筑、家具及其他器械的主要結(jié)構(gòu)方式，是在兩個(gè)構(gòu)件上采用凹凸部位相結(jié)合的一種連接方式．春秋時(shí)期著名的工匠魯班運(yùn)用榫卯結(jié)構(gòu)制作出了魯班鎖，且魯班鎖可拆解，但是要將它們拼接起來則需要較高的空間思維能力和足夠的耐心．如圖（1），六通魯班鎖是由六塊長度大小一樣，中間各有著不同鏤空的長條形木塊組裝而成．其主視圖如圖（2）所示，則其側(cè)視圖為（　　）
A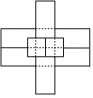． B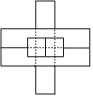． C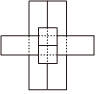． D．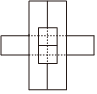
組卷：22引用：5難度：0.7
解析
4．函數(shù)f（x）為奇函數(shù)，g（x）為偶函數(shù)，在公共定義域內(nèi)，下列結(jié)論一定正確的是（　　）
A．f（x）+g（x）為奇函數(shù) B．f（x）+g（x）為偶函數(shù)
C．f（x）g（x）為奇函數(shù) D．f（x）g（x）為偶函數(shù)
組卷：190引用：8難度：0.8
解析
5．已知A（3，0），B（0，3），C（cosα，sinα），若
AC
?
BC
=
-
1
，則
sin
（
α
+
π
4
）
的值為（　　）
A．
2
3
B．
2
3
C．
2
2
D．
1
2
組卷：291引用：14難度：0.9
解析
6．若
0
＜
a
＜
1
2
，則
1
a
+
1
1
-
2
a
的最小值為（　　）
A．
3
+
2
2
B．
3
-
2
2
C．
4
2
D．4
組卷：245引用：3難度：0.6
解析
7．我國數(shù)學(xué)家陳景潤在哥德巴赫猜想的研究中取得了世界領(lǐng)先的成果．哥德巴赫猜想是“每個(gè)大于2的偶數(shù)可以表示為兩個(gè)素?cái)?shù)的和”，如20=3+17．在不超過15的素?cái)?shù)（素?cái)?shù)是指在大于1的自然數(shù)中，除了1和自身外沒有其他因數(shù)的自然數(shù)）中，隨機(jī)選取兩個(gè)不同的數(shù)，其和等于16的概率是（　　）
A．
1
10
B．
4
15
C．
2
15
D．
1
11
組卷：16引用：1難度：0.7
解析
8．某科技研發(fā)公司2021年全年投入的研發(fā)資金為300萬元，在此基礎(chǔ)上，計(jì)劃每年投入的研發(fā)資金比前一年增加10%，則該公司全年投入的研發(fā)資金開始超過600萬元的年份是（　　）
（參考數(shù)據(jù)：lg2=0.301，lg3=0.477，lg5=0.699，lg11=1.041．）
A．2027年 B．2028年 C．2029年 D．2030年
組卷：542引用：10難度：0.8
解析
9．已知{a_n}是等比數(shù)列，下列數(shù)列一定是等比數(shù)列的是（　　）
A．{ka_n}（k∈R） B．{a_n+a_n+1}
C．{a_n+1} D．{a_n+a_n+1+a_n+2}
組卷：49引用：1難度：0.7
解析
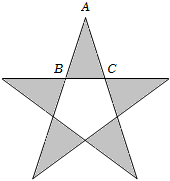10．十七世紀(jì)德國著名的天文學(xué)家開普勒曾經(jīng)這樣說過“幾何學(xué)里面有兩件寶，一個(gè)是勾股定理，一個(gè)是黃金分割，如果把勾股定理比作金礦的話，那么可以把黃金分割比作磚石”，黃金三角形有兩種，其中底與腰之比為黃金分割比的黃金三角形被認(rèn)為最美的三角形，它是一個(gè)頂角為36°的等腰三角形（另一種是頂角為108°的等腰三角形），如圖所示的五角星由五個(gè)黃金三角形與一個(gè)正五邊形組成，在其中一個(gè)黃金△ABC中，
BC
AC
=
5
-
1
2
，根據(jù)這些信息可得cos36°=（　　）
A．-
5
+
1
4
B．
2
5
-
1
4
C．
5
+
3
8
D．
5
+
1
4
組卷：35引用：3難度：0.6
解析
11．已知集合A={x|x²-x-6＜0}，B={x|2x+3＞1}，則A∪B=（　　）
A．（-1，3） B．（-2，+∞） C．（-2，-1） D．（-∞，-2）
組卷：84引用：2難度：0.9
解析

12．世界人口變化情況的三幅統(tǒng)計(jì)圖如圖所示．下列四個(gè)結(jié)論中錯(cuò)誤的是（　　）

A．從折線圖能看出世界人口的總量隨著年份的增加而增加

B．1957年到2050年各洲中北美洲人口增長速度最慢

C．2050年亞洲人口比其他各洲人口的總和還要多

D．2050年歐洲人口與南美洲及大洋洲人口之和基本持平

組卷：196引用：7難度：0.8

解析

二、填空題：本題共4小題，每小題5分，共20分.

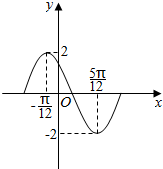13．函數(shù)y=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π）在一個(gè)周期內(nèi)的圖象如圖，此函數(shù)的解析式為
．
組卷：796引用：11難度：0.5
解析
14．已知向量
a
=
（
2
，
3
）
，
b
=
（
-
1
，
2
）
，則
a
在
b
方向上的投影向量的坐標(biāo)為
．
組卷：33引用：2難度：0.8
解析
15．設(shè)a＞b＞0，橢圓
x
2
a
2
+
y
2
b
2
=
1
的離心率為e₁，雙曲線
x
2
b
2
-
y
2
a
2
-
2
b
2
=
1
的離心率為e₂，若e₁e₂＜1，則
a
b
的取值范圍是
．
組卷：76引用：2難度：0.5
解析
16．已知球O的半徑為9，球心為O，球O被某平面所截得的截面為圓M，則以圓M為底面，O為頂點(diǎn)的圓錐的體積的最大值為
．
組卷：28引用：4難度：0.5
解析

三、解答題：共70分。解答應(yīng)寫出文字說明、證明過程或演算步驟。第17-21題為必考題，每個(gè)試題考生都必須作答.第22、23題為選考題，考生根據(jù)要求作答.

17．已知各項(xiàng)均為正數(shù)的數(shù)列{a_n}的前n項(xiàng)和為S_n，且
a
2
n
+
2
a
n
=
4
S
n
．
（1）求S_n；
（2）設(shè)
b
n
=
（
n
+
1
+
n
）
?
S
n
3
．且數(shù)列
{
1
b
n
}
的前n項(xiàng)和為T_n，求證：0＜3-T_n+1≤4cos50°-tan40°．
組卷：119引用：2難度：0.3
解析

18．2021年11月10日，在英國舉辦的《聯(lián)合國氣候變化框架公約》第26次締約方大會(huì)上，100多個(gè)國家政府、城市、州和主要企業(yè)簽署了《關(guān)于零排放汽車和面包車的格拉斯哥宣言》，以在2035年前實(shí)現(xiàn)在主要市場、2040年前在全球范圍內(nèi)結(jié)束內(nèi)燃機(jī)銷售，電動(dòng)汽車將成為汽車發(fā)展的大趨勢．電動(dòng)汽車生產(chǎn)過程主要包括動(dòng)力總成系統(tǒng)和整車制造及總裝．某企業(yè)計(jì)劃為某品牌電動(dòng)汽車專門制造動(dòng)力總成系統(tǒng)．
（1）動(dòng)力總成系統(tǒng)包括電動(dòng)機(jī)系統(tǒng)、電池系統(tǒng)以及電控系統(tǒng)，而且這三個(gè)系統(tǒng)的制造互不影響．已知在生產(chǎn)過程中，電動(dòng)機(jī)系統(tǒng)、電池系統(tǒng)以及電控系統(tǒng)產(chǎn)生次品的概率分別為
3
100
，
2
97
，
1
95
．
（ⅰ）求：在生產(chǎn)過程中，動(dòng)力總成系統(tǒng)產(chǎn)生次品的概率；
（ⅱ）動(dòng)力總成系統(tǒng)制造完成之后還要經(jīng)過檢測評(píng)估，此檢測程序需先經(jīng)過智能自動(dòng)化檢測，然后再進(jìn)行人工檢測，經(jīng)過兩輪檢測恰能檢測出所有次品，已知智能自動(dòng)化檢測的合格率為95%，求：在智能自動(dòng)化檢測為合格品的情況下，人工檢測一件產(chǎn)品為合格品的概率．
（2）隨著電動(dòng)汽車市場不斷擴(kuò)大，該企業(yè)通過技術(shù)革新提升了動(dòng)力總成系統(tǒng)的制造水平．現(xiàn)針對(duì)汽車?yán)m(xù)航能力的滿意度進(jìn)行用戶回訪．統(tǒng)計(jì)了100名用戶的數(shù)據(jù)，如下表：

對(duì)續(xù)航能能力是否滿意產(chǎn)品批次合計(jì)

技術(shù)革新之前技術(shù)革新之后

滿意 28 57 85

不滿意 12 3 15

合計(jì) 40 60 100

試問是否有99.9%的把握可以認(rèn)為用戶對(duì)續(xù)航能力的滿意度與該新款電動(dòng)汽車動(dòng)力總成系統(tǒng)的制造水平有關(guān)聯(lián)？
參考公式：
χ
2
=
n
（
ad
-
bc
）
2
（
a
+
b
）
（
c
+
d
）
（
a
+
c
）
（
b
+
d
）
，n=a+b+c+d

P（χ²≥x_a）=α 0.1 0.05 0.01 0.005 0.001

x_a 2.706 3.841 6.635 7.879 10.828

組卷：144引用：3難度：0.6

解析

19．如圖，三棱柱ABC-A₁B₁C₁中，側(cè)面BB₁C₁C為菱形，B₁C的中點(diǎn)為O，AC=AB₁．

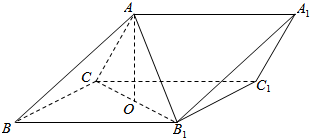
（1）文字?jǐn)⑹銎矫媾c平面垂直判定定理；
（2）求證：平面ABO⊥平面ACB₁．
組卷：29引用：1難度：0.3
解析
20．已知f（x）=ln（x+1）-x.
（1）求f（x）的單調(diào)區(qū)間；
（2）當(dāng)x＞0時(shí)，
k
x
2
e
x
-
1
-
x
≤
f
（
x
）
恒成立，求k的最大值．
組卷：52引用：3難度：0.6
解析
21．已知曲線C₁的直角坐標(biāo)方程為x²-y²=4，以直角坐標(biāo)原點(diǎn)O為極點(diǎn)，x軸的正半軸為極軸建立極坐標(biāo)系，曲線C₂的極坐標(biāo)方程為ρ=4cosθ．
（1）求C₁的極坐標(biāo)方程和C₂的直角坐標(biāo)方程；
（2）若曲線
θ
=
π
6
（
ρ
＞
0
）
與曲線C₁、曲線C₂分別交于兩點(diǎn)A、B，點(diǎn)P（4，0），求△PAB的面積．
組卷：33引用：3難度：0.5
解析

（二）選考題：共10分．請(qǐng)考生在第22、23題中任選一題作答．如果多做，則按所做的第一題計(jì)分．選修4-4：坐標(biāo)系與參數(shù)方程

22．（1）比較下列兩個(gè)代數(shù)式的大小：x²+5x+6與2x²+5x+9；
（2）若bc-ad≥0，bd＞0；求證：
a
+
b
b
≤
c
+
d
d
．
組卷：12引用：1難度：0.8
解析

選修4-5：不等式選講

23．已知拋物線E：x²=2py（p＞0）的焦點(diǎn)為F，A為E上一點(diǎn)，|AF|的最小值為1．
（1）求拋物線E的標(biāo)準(zhǔn)方程；
（2）過焦點(diǎn)F作互相垂直的兩條直線l₁，l₂，l₁與拋物線E相交于P，Q兩點(diǎn)，l₂與拋物線E相交于M，N兩點(diǎn)．若C，D分別是線段PQ，MN的中點(diǎn)，求|FC|²+|FD|²的最小值．
組卷：14引用：2難度：0.5
解析

0/60 進(jìn)入組卷

0/20 進(jìn)入試卷籃

布置作業(yè) 發(fā)布測評(píng) 反向細(xì)目表 平行組卷 下載答題卡 試卷分析 在線訓(xùn)練 收藏試卷

充值會(huì)員，資源免費(fèi)下載

A．f（x）+g（x）為奇函數(shù)	B．f（x）+g（x）為偶函數(shù)
C．f（x）g（x）為奇函數(shù)	D．f（x）g（x）為偶函數(shù)

A．{ka_n}（k∈R）	B．{a_n+a_n+1}
C．{a_n+1}	D．{a_n+a_n+1+a_n+2}

對(duì)續(xù)航能能力是否滿意	產(chǎn)品批次		合計(jì)
對(duì)續(xù)航能能力是否滿意	技術(shù)革新之前	技術(shù)革新之后	合計(jì)
滿意	28	57	85
不滿意	12	3	15
合計(jì)	40	60	100

P（χ²≥x_a）=α	0.1	0.05	0.01	0.005	0.001
x_a	2.706	3.841	6.635	7.879	10.828

2023年廣西名校高考數(shù)學(xué)聯(lián)考試卷（文科）（3月份）

一、選擇題：本題共12小題，每小題5分，共60分.在每小題給出的四個(gè)選項(xiàng)中，只有一項(xiàng)是符合題目要求的.

1．如果橢圓x2k+8+y29=1（k＞-8）的離心率為e=12，則k=（ ）

2．復(fù)數(shù)z滿足（1+i）z=i,則在復(fù)平面內(nèi)復(fù)數(shù)z所對(duì)應(yīng)的點(diǎn)位于（ ）

4．函數(shù)f（x）為奇函數(shù)，g（x）為偶函數(shù)，在公共定義域內(nèi)，下列結(jié)論一定正確的是（ ）

5．已知A（3，0），B（0，3），C（cosα，sinα），若AC?BC=-1，則sin（α+π4）的值為（ ）

6．若0＜a＜12，則1a+11-2a的最小值為（ ）

9．已知{an}是等比數(shù)列，下列數(shù)列一定是等比數(shù)列的是（ ）

11．已知集合A={x|x2-x-6＜0}，B={x|2x+3＞1}，則A∪B=（ ）

12．世界人口變化情況的三幅統(tǒng)計(jì)圖如圖所示．下列四個(gè)結(jié)論中錯(cuò)誤的是（ ）

二、填空題：本題共4小題，每小題5分，共20分.

13．函數(shù)y=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π）在一個(gè)周期內(nèi)的圖象如圖，此函數(shù)的解析式為．

14．已知向量a=（2，3），b=（-1，2），則a在b方向上的投影向量的坐標(biāo)為 ．

15．設(shè)a＞b＞0，橢圓x2a2+y2b2=1的離心率為e1，雙曲線x2b2-y2a2-2b2=1的離心率為e2，若e1e2＜1，則ab的取值范圍是 ．

16．已知球O的半徑為9，球心為O，球O被某平面所截得的截面為圓M，則以圓M為底面，O為頂點(diǎn)的圓錐的體積的最大值為 ．

三、解答題：共70分。解答應(yīng)寫出文字說明、證明過程或演算步驟。第17-21題為必考題，每個(gè)試題考生都必須作答.第22、23題為選考題，考生根據(jù)要求作答.

17．已知各項(xiàng)均為正數(shù)的數(shù)列{an}的前n項(xiàng)和為Sn，且a2n+2an=4Sn．（1）求Sn；（2）設(shè)bn=（n+1+n）?Sn3．且數(shù)列{1bn}的前n項(xiàng)和為Tn，求證：0＜3-Tn+1≤4cos50°-tan40°．

19．如圖，三棱柱ABC-A1B1C1中，側(cè)面BB1C1C為菱形，B1C的中點(diǎn)為O，AC=AB1．（1）文字?jǐn)⑹銎矫媾c平面垂直判定定理；（2）求證：平面ABO⊥平面ACB1．

20．已知f（x）=ln（x+1）-x.（1）求f（x）的單調(diào)區(qū)間；（2）當(dāng)x＞0時(shí)，kx2ex-1-x≤f（x）恒成立，求k的最大值．

（二）選考題：共10分．請(qǐng)考生在第22、23題中任選一題作答．如果多做，則按所做的第一題計(jì)分．選修4-4：坐標(biāo)系與參數(shù)方程

22．（1）比較下列兩個(gè)代數(shù)式的大小：x2+5x+6與2x2+5x+9；（2）若bc-ad≥0，bd＞0；求證：a+bb≤c+dd．

選修4-5：不等式選講

1．如果橢圓
x
2
k
+
8
+
y
2
9
=
1
（
k
＞
-
8
）
的離心率為e=
1
2
，則k=（　　）

2．復(fù)數(shù)z滿足（1+i）z=i,則在復(fù)平面內(nèi)復(fù)數(shù)z所對(duì)應(yīng)的點(diǎn)位于（　　）

4．函數(shù)f（x）為奇函數(shù)，g（x）為偶函數(shù)，在公共定義域內(nèi)，下列結(jié)論一定正確的是（　　）

5．已知A（3，0），B（0，3），C（cosα，sinα），若
AC
?
BC
=
-
1
，則
sin
（
α
+
π
4
）
的值為（　　）

6．若
0
＜
a
＜
1
2
，則
1
a
+
1
1
-
2
a
的最小值為（　　）

9．已知{a_n}是等比數(shù)列，下列數(shù)列一定是等比數(shù)列的是（　　）

11．已知集合A={x|x²-x-6＜0}，B={x|2x+3＞1}，則A∪B=（　　）

12．世界人口變化情況的三幅統(tǒng)計(jì)圖如圖所示．下列四個(gè)結(jié)論中錯(cuò)誤的是（　　）

13．函數(shù)y=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π）在一個(gè)周期內(nèi)的圖象如圖，此函數(shù)的解析式為
．

14．已知向量
a
=
（
2
，
3
）
，
b
=
（
-
1
，
2
）
，則
a
在
b
方向上的投影向量的坐標(biāo)為
．

15．設(shè)a＞b＞0，橢圓
x
2
a
2
+
y
2
b
2
=
1
的離心率為e₁，雙曲線
x
2
b
2
-
y
2
a
2
-
2
b
2
=
1
的離心率為e₂，若e₁e₂＜1，則
a
b
的取值范圍是
．

16．已知球O的半徑為9，球心為O，球O被某平面所截得的截面為圓M，則以圓M為底面，O為頂點(diǎn)的圓錐的體積的最大值為
．

17．已知各項(xiàng)均為正數(shù)的數(shù)列{a_n}的前n項(xiàng)和為S_n，且
a
2
n
+
2
a
n
=
4
S
n
．
（1）求S_n；
（2）設(shè)
b
n
=
（
n
+
1
+
n
）
?
S
n
3
．且數(shù)列
{
1
b
n
}
的前n項(xiàng)和為T_n，求證：0＜3-T_n+1≤4cos50°-tan40°．

19．如圖，三棱柱ABC-A₁B₁C₁中，側(cè)面BB₁C₁C為菱形，B₁C的中點(diǎn)為O，AC=AB₁．

（1）文字?jǐn)⑹銎矫媾c平面垂直判定定理；
（2）求證：平面ABO⊥平面ACB₁．

20．已知f（x）=ln（x+1）-x.
（1）求f（x）的單調(diào)區(qū)間；
（2）當(dāng)x＞0時(shí)，
k
x
2
e
x
-
1
-
x
≤
f
（
x
）
恒成立，求k的最大值．

22．（1）比較下列兩個(gè)代數(shù)式的大小：x²+5x+6與2x²+5x+9；
（2）若bc-ad≥0，bd＞0；求證：
a
+
b
b
≤
c
+
d
d
．