2023-2024學年湖北省恩施州宣恩縣清源自然雙語高級中學高三(上)期中數學試卷
發布:2025/6/29 7:0:12
一、單項選擇題:本題共8小題,每小題5分,共40分.在每小題給出的四個選項中,只有一項是符合題目要求的.
-
1.已知函數
在(0,1)內單調遞增,則實數a的取值范圍是( )f(x)=x(x-a)A.a≥2 B.a≥0 C.a≤2 D.a≤0 組卷:44引用:2難度:0.8 -
2.若復數z滿足(1+i)z=|1+i|,則
的虛部為( )zA. -2iB. -22C. 22iD. 22組卷:64引用:1難度:0.7 -
3.《周髀算經》中有這樣一個問題:從冬至日起,依次有小寒、大寒、立春、雨水、驚蟄、春分、清明、谷雨、立夏、小滿、芒種這十二個節氣其日影長依次成等差數列.若冬至、立春、春分日影長之和為31.5尺,谷雨日影長為5.5尺,則這十二個節氣日影長之和為( )
A.80尺 B.96尺 C.162尺 D.228尺 組卷:502引用:3難度:0.5 -
4.已知空間中不過同一點的三條直線l,m,n,條件“l,m,n共面”成立的一個充分不必要條件是( )
A.l∩m=P,l∩n=Q B.l,m,n兩兩相交 C.l∥m,l∥n D.l∥m,m∩n=P 組卷:94引用:2難度:0.7 -
5.命題“?x∈R,x2+1>0”的否定是( )
A.?x∈R,x2+1<0 B.?x∈R,x2+1≤0 C.?x∈R,x2+1≤0 D.?x∈R,x2+1<0 組卷:221引用:23難度:0.9 -
6.已知函數
為f(x)的導函數,則y=f'(x)的大致圖象是( )f(x)=16x3+sinx,f′(x)A. 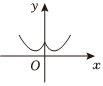
B. 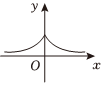
C. 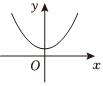
D. 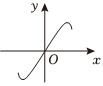 組卷:63引用:1難度:0.4
組卷:63引用:1難度:0.4 -
7.不等式1+5x-6x2<0的解集為( )
A.{x|x>1或 }x<-16B. {x|-16<x<1}C.{x|x>2或x<-3} D.{x|-3<x<2} 組卷:26引用:4難度:0.5 -
8.系統找不到該試題
二、多項選擇題:本題共4小題,每小題5分,共20分。在每小題給出的四個選項中,有多項符合題目要求.全部選對的得5分,部分選對的得2分,有選錯的得0分.
-
9.若a,b,c∈R,則下列命題正確的是( )
A.若ab≠0且a<b,則 1a>1bB.若0<a<1,則a2<a C.若a>b>0且c>0,則 b+ca+c>baD.a2+b2+1≥2(a-2b-2) 組卷:290引用:12難度:0.8 -
10.設定義在R上的函數f(x),g(x)滿足:①g(0)=1:②對任意實數x1,x2滿足g(x1-x2)=f(x1)f(x2)+g(x1)g(x2);③存在大于零的常數m,使得f(m)=1,且當x∈(0,m)時,f(x)>0,g(x)>0.則( )
A.g(m)=f(0)=0 B.當x∈(0,m)時,f(x)+g(x)>1 C.函數f(x)?g(x)在R上沒有最值 D.任取x∈R,f(m-x)=g(x) 組卷:154引用:2難度:0.3 -
 11.中國傳統文化中很多內容體現了數學的“對稱美”,如圖所示的太極圖是由黑白兩個魚形紋組成的圖案,俗稱陰陽魚,太極圖展現了一種相互轉化,相對統一的和諧美.定義:圓O的圓心在原點,若函數的圖象將圓O的周長和面積同時等分成兩部分,則這個函數稱為圓O的一個“太極函數”,則下列說法正確的是( )
11.中國傳統文化中很多內容體現了數學的“對稱美”,如圖所示的太極圖是由黑白兩個魚形紋組成的圖案,俗稱陰陽魚,太極圖展現了一種相互轉化,相對統一的和諧美.定義:圓O的圓心在原點,若函數的圖象將圓O的周長和面積同時等分成兩部分,則這個函數稱為圓O的一個“太極函數”,則下列說法正確的是( )A.對于圓O,其“太極函數”有且只有1個 B.函數 是圓O的一個“太極函數”f(x)=x2-x(x≥0)-x2-x(x<0)C.函數f(x)=x3-3x不是圓O的“太極函數” D.函數 是圓O的一個“太極函數”f(x)=ln(x2+1+x)組卷:73引用:1難度:0.5 -
12.有一組樣本數據x1,x2,?,xn,其平均數和方差分別為
,s2.由這組數據得到一組新樣本數據y1,y2,?,yn,其中yi=2xi+3(i=1,2,?,n),其平均數和方差分別為x,s'2,則( )yA. y=2xB.s2=s'2 C. x=12y-32D. s2=14s′2組卷:13引用:2難度:0.7
三、填空題:本題共4小題,每小題5分,共20分.
-
13.函數
的最小正周期為 .y=sin(2x+π3)+4組卷:124引用:2難度:0.9 -
14.設Sn為等差數列{an}(n∈N*)的前n項和,若S10=20,S20=10,且Sn=-30,則n的值為.
組卷:135引用:3難度:0.7 -
15.某單位安排A,B,C,D,E,F等6名工作人員到4個不同的地方開展工作,每個地方至少需安排一名工作人員,其中A,B被安排到同一個地方工作,D,E不能被安排到同一個地方工作,則不同的分配方法共有 種.
組卷:126引用:2難度:0.8 -
16.已知△ABC,點D滿足
,若2BD=3DC,則μ=.AD=λAB+μAC(λ,μ∈R)組卷:34引用:1難度:0.7
四、解答題:本題共6小題,共70分。解答應寫出文字說明、證明過程或演算步驟.
-
17.已知
.f(α)=cos(3π-α)sin(α+π2)sin(π-α)tan(2π-α)cos(32π-α)cos(π+α)
(1)若,求f(α-π4)=35,α∈(3π4,5π4)的值.sin(π4+α)
(2)已知.求角β的值.0<α<π2<β<π,f(α)=45,cos(β-α)=210組卷:100引用:3難度:0.6 -
18.已知數列{an}的前n項和為Sn,a1=-
,且4Sn+1=3Sn-9.94
(1)求數列{an}的通項公式;
(2)設數列{bn}滿足3bn+nan=0(n∈N*),記數列{bn}的前n項和為Tn,若Tn≤λbn+12對任意n∈N*恒成立,求實數λ的取值范圍.組卷:253引用:7難度:0.5 -
 19.為迎接建黨一百周年,在全縣中小學校開展“恰是百年風華,愛我山河美景”競賽考試活動,進一步激發學生的愛國熱情.某中學于2021年3月份對全校學生進行了“建黨一百周年”國防教育知識競賽考試,并隨機抽取了100名學生的成績進行了統計,其中男女生各占一半,繪制了頻率分布直方圖(如圖所示),規定80分(滿分100分)及以上者為成績優秀,否則為成績不優秀.
19.為迎接建黨一百周年,在全縣中小學校開展“恰是百年風華,愛我山河美景”競賽考試活動,進一步激發學生的愛國熱情.某中學于2021年3月份對全校學生進行了“建黨一百周年”國防教育知識競賽考試,并隨機抽取了100名學生的成績進行了統計,其中男女生各占一半,繪制了頻率分布直方圖(如圖所示),規定80分(滿分100分)及以上者為成績優秀,否則為成績不優秀.
(1)求圖中a的值;
(2)根據已知條件完成下面2×2列聯表,并判斷能否有95%的把握認為“成績優秀”與性別有關?
(3)將頻率視為概率,從本次考試的全縣所有學生中,隨機抽取4人去其他學校進行愛國勵志演講宣傳,記抽取的4人中成績優秀的人數為X,求X的分布列和數學期望.成績優秀 成績不優秀 合計 男 17 女 50 合計
附:P(K2≥k) … 0.10 0.05 0.025 0.010 0.001 k … 2.706 3.841 5.024 6.635 10.828 .K2=n(ad-bc)2(a+b)(c+d)(a+c)(b+d)組卷:60引用:4難度:0.5 -
20.設
曲線y=f(x)在點(1,f(1))處取得極值.f(x)=alnx+12x-32x+1
(1)求a的值;
(2)求函數f(x)的單調區間和極值.組卷:815引用:13難度:0.6 -
21.如圖所示的五邊形SBADC中ABCD是矩形,AD=2AB,SB=SC,沿BC折疊成四棱錐S-ABCD,MB=MC,SM=2.

(1)從條件①;②sin∠SBM=255;③cos∠SAM=33中任選兩個作為補充條件,證明:平面SBC⊥平面ABCD;SA=6
(2)在(1)的條件下,求點C到平面SAD的距離.組卷:6引用:1難度:0.4 -
22.在△ABC中,A,B,C的對邊分別為a,b,c,acosB-2acosC=(2c-b)cosA.
(1)若c=a,求cosB的值;3
(2)若b=1,∠BAC的平分線AD交BC于點D,求AD長度的取值范圍.組卷:1732引用:13難度:0.6


