人教B版(2019)選擇性必修第一冊(cè)《第一章 空間向量與立體幾何》2021年單元測(cè)試卷(4)
發(fā)布:2025/6/29 8:0:17
一、單選題(本大題共8小題,每小題5分,共50分,在每小題給出的四個(gè)選項(xiàng)中,只有一個(gè)是符合題目要求的)
-
1.已知圓C:x2+y2-6x-4y+12=0,M,N是圓上的兩點(diǎn),點(diǎn)A(1,0),且
,則AM=λAN的值為( )AM?ANA. 7B.7 C. 22D.8 組卷:47引用:3難度:0.5 -
2.已知空間向量
=(2,-1,1),a=(-4,x,y),b∥a,則x-y=( )bA.4 B.-4 C.0 D.2 組卷:167引用:2難度:0.9 -
3.已知空間三點(diǎn)A(1,-1,2),B(3,0,-1),C(2,3,-3),則向量
與AB的夾角為( )CBA. π6B. π3C. 2π3D. 5π6組卷:231引用:7難度:0.7 -
 4.如圖,已知正方體ABCD-A1B1C1D1的棱長(zhǎng)為2,點(diǎn)P是四邊形A1B1C1D1的內(nèi)切圓上一點(diǎn),O為四邊形ABCD的中心,則的最大值為( )OP?DP
4.如圖,已知正方體ABCD-A1B1C1D1的棱長(zhǎng)為2,點(diǎn)P是四邊形A1B1C1D1的內(nèi)切圓上一點(diǎn),O為四邊形ABCD的中心,則的最大值為( )OP?DPA.5 B.6 C. 5+2D. 5+3組卷:717引用:4難度:0.5 -
5.設(shè)x,y∈R,向量
,a=(x,1,1),b=(1,y,1),且c=(3,-6,3),a⊥c,則b∥c=( )|a+b|A. 10B.3 C.4 D. 22組卷:315引用:11難度:0.7 -
6.已知正方體ABCD-A1B1C1D1中,AB=2,則點(diǎn)C到平面BDD1B1的距離為( )
A.1 B. 2C.2 2D.2 3組卷:215引用:4難度:0.7 -
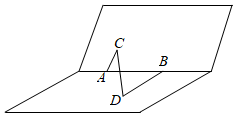 7.如圖在一個(gè)120°的二面角的棱上有兩點(diǎn)A,B,線段AC,BD分別在這個(gè)二面角的兩個(gè)半平面內(nèi),且均與棱AB垂直,若CD=3,AC=1,BD=2,則AB的長(zhǎng)為( )
7.如圖在一個(gè)120°的二面角的棱上有兩點(diǎn)A,B,線段AC,BD分別在這個(gè)二面角的兩個(gè)半平面內(nèi),且均與棱AB垂直,若CD=3,AC=1,BD=2,則AB的長(zhǎng)為( )A. 2B.2 C. 6D.6 組卷:242引用:3難度:0.6 -
8.正三棱錐V-ABC(頂點(diǎn)在底面的射影是底面正三角形的中心)中,D,E,F(xiàn)分別是VC,VA,AC的中點(diǎn),P為VB上任意一點(diǎn),則直線DE與PF所成的角的大小是( )
A.30° B.90° C.60° D.隨P點(diǎn)的變化而變化 組卷:182引用:25難度:0.9
二、多選題(本大題共4小題,每小題5分,共10分,在每小題給出的選項(xiàng)中,有多個(gè)選項(xiàng)符合題目要求,全部選對(duì)的得5分,有選錯(cuò)的得0分,部分選對(duì)的得3分)
-
9.已知空間中三點(diǎn)A(0,1,0),B(2,2,0),C(-1,3,1),則下列說(shuō)法正確的是( )
A. 與AB是共線向量ACB.與 同向的單位向量是(AB,255,0)55C. 和AB夾角的余弦值是BC5511D.平面ABC的一個(gè)法向量是(1,-2,5) 組卷:657引用:31難度:0.7 -
10.若正四棱錐的體積為18,則當(dāng)該正四棱錐的側(cè)面積最小時(shí),下列結(jié)論中正確的有( )
A.棱錐的高與底面邊長(zhǎng)的比值為 22B.側(cè)棱與底面所成的角為 π4C.棱錐的高與底面邊長(zhǎng)的比值為 2D.側(cè)棱與底面所成的角為 π3組卷:5引用:2難度:0.9 -
11.已知
為直線l的方向向量,v,n1分別為平面α,β的法向量(α,β不重合),那么下列說(shuō)法中,正確的有( )n2A. ∥n1?α∥βn2B. ⊥n1?α⊥βn2C. ∥v?l∥αn1D. ⊥v?l⊥αn1組卷:283引用:24難度:0.6 -
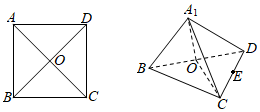 12.如圖,將邊長(zhǎng)為2的正方形ABCD沿對(duì)角線BD折起,得到三棱錐A1-BCD,則下列命題中,正確的為( )
12.如圖,將邊長(zhǎng)為2的正方形ABCD沿對(duì)角線BD折起,得到三棱錐A1-BCD,則下列命題中,正確的為( )A.直線BD⊥平面A1OC B.三棱錐A1-BCD的外接球的表面積是8π C.A1B⊥CD D.若E為CD的中點(diǎn),則A1B⊥平面A1OE 組卷:85引用:5難度:0.5
三、填空題(本大題共4小題,每小題5分,共20分,將答案填在題中橫線處)
-
13.已知向量
,a滿足b,|a|=1,|b|=2.則|a+2b|=5=.a?b組卷:4引用:2難度:0.8 -
14.已知
,若a=(2,-1,3),b=(-1,4,2),c=(-3,5,λ)三向量共面,則實(shí)數(shù)λ=.a,b,c組卷:624引用:10難度:0.8 -
15.如圖,PA⊥平面ABC,AC⊥BC,PA=AC=1,BC=
,則二面角A-PB-C的余弦值大小為.2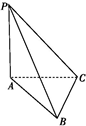 組卷:164引用:3難度:0.5
組卷:164引用:3難度:0.5 -
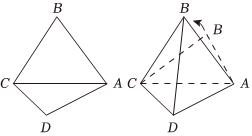 16.平面四邊形ABCD中,AB=BC=CA=2,AD=DC,∠CDA=90°,把三角形ABC沿AC折起,使得三角形ABC所在平面與三角形ACD所在平面垂直,連接BD,則直線BD與平面ACD所成角的余弦值為 ,點(diǎn)C到平面ABD的距離為 .組卷:12引用:1難度:0.5
16.平面四邊形ABCD中,AB=BC=CA=2,AD=DC,∠CDA=90°,把三角形ABC沿AC折起,使得三角形ABC所在平面與三角形ACD所在平面垂直,連接BD,則直線BD與平面ACD所成角的余弦值為 ,點(diǎn)C到平面ABD的距離為 .組卷:12引用:1難度:0.5
四、解答題(共大題共6小題,共70分.解答應(yīng)寫出必要的文字說(shuō)明、證明過(guò)程或演算步驟)
-
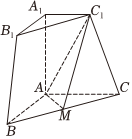 17.如圖,在三棱臺(tái)ABC-A1B1C1中,若A1A⊥平面ABC,AB⊥AC,AB=AC=AA1=2,A1C1=1,M為棱BC上一動(dòng)點(diǎn)(不包含端點(diǎn)).
17.如圖,在三棱臺(tái)ABC-A1B1C1中,若A1A⊥平面ABC,AB⊥AC,AB=AC=AA1=2,A1C1=1,M為棱BC上一動(dòng)點(diǎn)(不包含端點(diǎn)).
(1)若M為BC的中點(diǎn),在圖中過(guò)點(diǎn)A1作一個(gè)平面α,使得平面C1MA∥α.(不必給出證明過(guò)程,只要求作出α與棱臺(tái)ABCD-A1B1C1D1的截面);
(2)是否存在點(diǎn)M,使得平面C1MA與平面ACC1A1所成角的余弦值為?若存在,求出BM長(zhǎng)度;若不存在,請(qǐng)說(shuō)明理由.66組卷:26引用:2難度:0.4 -
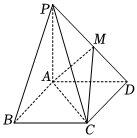 18.如圖,在四棱線P-ABCD中,底面ABCD為矩形,PA⊥平面ABCD,PA=AD=AB,點(diǎn)M是棱PD的中點(diǎn).2
18.如圖,在四棱線P-ABCD中,底面ABCD為矩形,PA⊥平面ABCD,PA=AD=AB,點(diǎn)M是棱PD的中點(diǎn).2
(Ⅰ)求證:PB∥平面ACM;
(Ⅱ)設(shè)AC的中點(diǎn)為O,點(diǎn)N在棱PC上(異于點(diǎn)P,C),且ON=OA,求直線AN與平面ACM所成角的正弦值.組卷:87引用:1難度:0.5 -
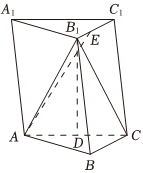 19.如圖,在三棱柱ABC-A1B1C1中,B1A=B1C,AA1=13,AB=8,BC=6,AB⊥BC,D為AC中點(diǎn),tan∠BB1D=.512
19.如圖,在三棱柱ABC-A1B1C1中,B1A=B1C,AA1=13,AB=8,BC=6,AB⊥BC,D為AC中點(diǎn),tan∠BB1D=.512
(1)求證:BC⊥B1D;
(2)線段B1C1上是否存在一點(diǎn)E,使得AE與面BCC1B1的夾角正弦值為.1274185組卷:64引用:4難度:0.4 -
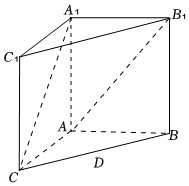 20.如圖,在直三棱柱ABC-A1B1C1中,AA1=AC=4,AB=3,BC=5,點(diǎn)D是線段BC的中點(diǎn).
20.如圖,在直三棱柱ABC-A1B1C1中,AA1=AC=4,AB=3,BC=5,點(diǎn)D是線段BC的中點(diǎn).
(1)求證:AB⊥A1C;
(2)求二面角D-CA1-A的余弦值.組卷:339引用:6難度:0.6 -
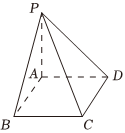 21.如圖,P-ABCD為四棱錐.
21.如圖,P-ABCD為四棱錐.
(1)若=mPD+nPA+tPB,求證:m+n+t=1;PC
(2)若P-ABCD為正四棱錐,且PA=AB=,求底面中心O到面PCD的距離.(要求用向量知識(shí)求解)2組卷:2引用:1難度:0.6 -
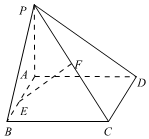 22.如圖,已知矩形ABCD所在平面外一點(diǎn)P,PA⊥平面ABCD,E、F分別是AB、PC的中點(diǎn).
22.如圖,已知矩形ABCD所在平面外一點(diǎn)P,PA⊥平面ABCD,E、F分別是AB、PC的中點(diǎn).
(1)求證:共面;EF,AP,AD
(2)求證:EF⊥CD.組卷:425引用:6難度:0.5


