當(dāng)前位置：試卷中心 > 試卷詳情

2020-2021學(xué)年江西省宜春市銅鼓中學(xué)非實(shí)驗(yàn)班高二（下）開(kāi)學(xué)數(shù)學(xué)試卷（理科）

發(fā)布：2025/6/29 9:0:20

一、選擇題：本大題共12小題，每小題5分，共60分。在每小題給出的四個(gè)選項(xiàng)中，只有一項(xiàng)是符合題目要求的。

1．給出下列四個(gè)命題，其中正確的命題是（　　）
①平行于同一直線的兩條直線平行；
②平行于同一平面的兩條直線平行；
③平行于同一直線的兩個(gè)平面平行；
④平行于同一平面的兩個(gè)平面平行．
A．①② B．③④ C．①④ D．②③
組卷：120引用：3難度：0.7
解析
2．已知角α的終邊經(jīng)過(guò)點(diǎn)P（-3，-4），則
cos
（
3
2
π
-
α
）
的值等于（　　）
A．
-
3
5
B．
-
4
5
C．
3
5
D．
4
5
組卷：277引用：3難度：0.8
解析
3．在△ABC中，a=2，
B
=
π
3
，△ABC的面積等于
3
2
，則b等于（　　）
A．
3
2
B．1 C．
3
D．2
組卷：103引用：7難度：0.7
解析

4．設(shè)A₁、A₂、A₃、A₄為平面直角坐標(biāo)系中兩兩不同的點(diǎn)，若
A
1
A
3
=
λ
A
1
A
2
（
λ
∈
R
）
，
A
1
A
4
=
μ
A
1
A
2
（
μ
∈
R
）
，且
1
λ
+
1
μ
=
4
，則稱點(diǎn)A₃、A₄和諧分割點(diǎn)A₁、A₂.已知平面上兩兩不同的點(diǎn)A、B、C、D，若C、D和諧分割點(diǎn)A、B．則下面說(shuō)法正確的是（　　）

A．點(diǎn)C可能是線段AB的中點(diǎn)

B．點(diǎn)C可能是靠近點(diǎn)A的線段AB的三等分點(diǎn)

C．點(diǎn)C、D可能同時(shí)在線段AB上

D．點(diǎn)C、D可能同時(shí)在線段AB的延長(zhǎng)線上

組卷：128引用：3難度：0.5

解析

5．已知1≤a≤4，-1≤b≤2，則3a-b的取值范圍是（　　）
A．-13≤3a-b≤1 B．-1≤3a-b≤8 C．-1≤3a-b≤13 D．1≤3a-b≤13
組卷：104引用：12難度：0.8
解析

6．已知f（x）=2sin3x,則下列說(shuō)法正確的是（　　）

A．f（x）的圖象關(guān)于直線x=π對(duì)稱

B．f（x）在

[

，

]

上單調(diào)遞增

C．f（x）在

[

，

]

上的值域?yàn)?div dealflag="1" class="MathJye" mathtag="math">

[

，

]

D．f（x）圖象可由

（

）

sin

（

）

的圖象向右平移

個(gè)單位長(zhǎng)度得到

組卷：195引用：2難度：0.5

解析

7．已知
a
，
b
是單位向量，且
2
a
+
b
=
（

-
3

，

1

）
，則
|

a
-
b

|
=（　　）
A．2 B．
5
C．1 D．
10
2
組卷：160引用：3難度：0.7
解析
8．不等式-2x²+x+3≤0的解集是（　　）
A．
{
x
|
-
1
≤
x
≤
3
2
}
B．{x|x≤-1或x≥
3
2
}
C．{x|x≤-
3
2
或x≥1} D．
{
x
|
-
3
2
≤
x
≤
1
}
組卷：179引用：3難度：0.8
解析
9．已知等差數(shù)列{a_n}的前n項(xiàng)和為S_n，若S₉=54，S₈-S₅=30，則S₁₁=（　　）
A．77 B．88 C．99 D．110
組卷：267引用：3難度：0.8
解析
10．已知數(shù)列{a_n}滿足a₁=1，a_n+1=2a_n，則a₄=（　　）
A．4 B．8 C．16 D．32
組卷：431引用：3難度：0.8
解析
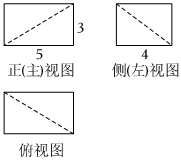11．若一個(gè)幾何體的三視圖如圖所示，則該幾何體的體積為（　　）
A．40 B．50 C．30 D．45
組卷：42引用：3難度：0.6
解析
12．系統(tǒng)找不到該試題

二、填空題（本大題共4小題，每小題5分，共20分）

13．定義：[x]（x∈R）表示不超過(guò)x的最大整數(shù)．例如[1.5]=1，[-0.5]=-1．給出下列結(jié)論：
①函數(shù)y=[sinx]是周期為2π的周期函數(shù)；
②函數(shù)y=[sinx]是奇函數(shù)；
③函數(shù)y=[sinx]的值域是{-1，0，1}；
④函數(shù)y=[sinx]-cosx不存在零點(diǎn)．
其中正確命題的序號(hào)是

（寫出所有正確命題的序號(hào)）．
組卷：21引用：2難度：0.5
解析
14．已知函數(shù)f（x）是定義在R上的奇函數(shù)，且當(dāng)x＞0時(shí)，f（x）=cos3x+sin2x,則當(dāng)x＜0時(shí)，f（x）的表達(dá)為
．
組卷：224引用：2難度：0.5
解析
15．△ABC?的外心為O?，三個(gè)內(nèi)角A，B，C?所對(duì)的邊分別為
a
,
b
,
c
,
AO
?
BC
=
1
2
a
（
a
-
8
5
c
）
?，b=4?．則△ABC?面積的最大值為
．
組卷：404引用：6難度：0.4
解析
16．若x＞1，則x+
1
x
-
1
的最小值是
．
組卷：1509引用：40難度：0.7
解析

三、解答題：共70分。解答應(yīng)寫出文字說(shuō)明、證明過(guò)程或演算步驟。

17．已知向量
a
，
b
滿足
|
a
|
=
1
，
|
b
|
=
2
，
（
2
a
-
b
）
?
（
a
+
2
b
）
=
1
．
（1）求
a
與
b
的夾角θ；
（2）求
|
a
-
2
b
|
的值．
組卷：22引用：1難度：0.6
解析
18．在△ABC中，角A，B，C的對(duì)邊分別為a,b,c,且
tan
A
tan
B
=
2
c
-
b
b
．
（Ⅰ）求角A的大小；
（Ⅱ）若a=2，求△ABC面積的最大值及此時(shí)邊b,c的值．
組卷：207引用：4難度：0.9
解析
19．已知a,b為兩條異面直線，α為平面，且a⊥b,a⊥α，b?α．
（1）若直線c∥a,通過(guò)直線與平面垂直的判定定理，證明：c⊥α；
（2）用反證法證明：b∥α．
組卷：42引用：1難度：0.7
解析
20．設(shè)n次多項(xiàng)式T_n（x）=a_nxⁿ+a_n-1x^n-1+?+a₂x²+a₁x¹+a₀，（a_n≠0），若其滿足T_n（cosθ）=cosnθ，則稱這些多項(xiàng)式T_n（x）為切比雪夫多項(xiàng)式．例如：由cos2θ=2cos²θ-1可得切比雪夫多項(xiàng)式T₂（x）=2x²-1．
（1）求切比雪夫多項(xiàng)式T₃（x）；
（2）求sin18°的值；
（3）已知方程8x³-6x-1=0在（-1，1）上有三個(gè)不同的根，記為x₁，x₂，x₃，求證：x₁+x₂+x₃=0．
組卷：295引用：2難度：0.1
解析
21．在等差數(shù)列{a_n}中，S_n為其前n項(xiàng)和（n∈N₊）．若a₂=3，S₄=16．
（1）求數(shù)列{a_n}的通項(xiàng)公式；
（2）設(shè)
b
n
=
1
a
n
?
a
n
+
1
，求數(shù)列{b_n}的前n項(xiàng)和T_n．
組卷：165引用：5難度：0.6
解析
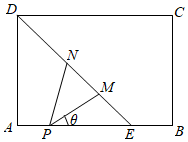22．如圖，矩形ABCD是一個(gè)歷史文物展覽廳的俯視圖，點(diǎn)E在AB上，在梯形BCDE區(qū)域內(nèi)部展示文物，DE是玻璃幕墻，游客只能在△ADE區(qū)域內(nèi)參觀在AE上的點(diǎn)P處安裝一可旋轉(zhuǎn)的監(jiān)控?cái)z像頭，∠MPN為監(jiān)控角，其中M，N在線段D，E（含端點(diǎn)）上，且點(diǎn)M在點(diǎn)N的右下方，經(jīng)測(cè)量得知：AD=8米，AE=8米，AP=2米，
∠
MPN
=
π
4
．記∠EPM=θ，監(jiān)控?cái)z像頭的可視區(qū)域△PMN的面積為S平方米．
（1）求S關(guān)于θ的函數(shù)關(guān)系式，并寫出cosθ的取值范圍；
（2）求可視區(qū)域△PMN的面積的最小值．
組卷：237引用：3難度：0.5
解析

0/60 進(jìn)入組卷

0/20 進(jìn)入試卷籃

布置作業(yè) 發(fā)布測(cè)評(píng) 反向細(xì)目表 平行組卷 下載答題卡 試卷分析 在線訓(xùn)練 收藏試卷

充值會(huì)員，資源免費(fèi)下載

A． { x \| - 1 ≤ x ≤ 3 2 }	B．{x\|x≤-1或x≥ 3 2 }
C．{x\|x≤- 3 2 或x≥1}	D． { x \| - 3 2 ≤ x ≤ 1 }

2020-2021學(xué)年江西省宜春市銅鼓中學(xué)非實(shí)驗(yàn)班高二（下）開(kāi)學(xué)數(shù)學(xué)試卷（理科）

一、選擇題：本大題共12小題，每小題5分，共60分。在每小題給出的四個(gè)選項(xiàng)中，只有一項(xiàng)是符合題目要求的。

1．給出下列四個(gè)命題，其中正確的命題是（ ）①平行于同一直線的兩條直線平行；②平行于同一平面的兩條直線平行；③平行于同一直線的兩個(gè)平面平行；④平行于同一平面的兩個(gè)平面平行．

2．已知角α的終邊經(jīng)過(guò)點(diǎn)P（-3，-4），則cos（32π-α）的值等于（ ）

3．在△ABC中，a=2，B=π3，△ABC的面積等于32，則b等于（ ）

5．已知1≤a≤4，-1≤b≤2，則3a-b的取值范圍是（ ）

6．已知f（x）=2sin3x,則下列說(shuō)法正確的是（ ）

7．已知a，b是單位向量，且2a+b=（ -3 ， 1 ），則| a-b |=（ ）

8．不等式-2x2+x+3≤0的解集是（ ）

9．已知等差數(shù)列{an}的前n項(xiàng)和為Sn，若S9=54，S8-S5=30，則S11=（ ）

10．已知數(shù)列{an}滿足a1=1，an+1=2an，則a4=（ ）

11．若一個(gè)幾何體的三視圖如圖所示，則該幾何體的體積為（ ）

二、填空題（本大題共4小題，每小題5分，共20分）

14．已知函數(shù)f（x）是定義在R上的奇函數(shù)，且當(dāng)x＞0時(shí)，f（x）=cos3x+sin2x,則當(dāng)x＜0時(shí)，f（x）的表達(dá)為．

15．△ABC?的外心為O?，三個(gè)內(nèi)角A，B，C?所對(duì)的邊分別為a,b,c,AO?BC=12a（a-85c）?，b=4?．則△ABC?面積的最大值為 ．

16．若x＞1，則x+1x-1的最小值是．

三、解答題：共70分。解答應(yīng)寫出文字說(shuō)明、證明過(guò)程或演算步驟。

17．已知向量a，b滿足|a|=1，|b|=2，（2a-b）?（a+2b）=1．（1）求a與b的夾角θ；（2）求|a-2b|的值．

18．在△ABC中，角A，B，C的對(duì)邊分別為a,b,c,且tanAtanB=2c-bb．（Ⅰ）求角A的大小；（Ⅱ）若a=2，求△ABC面積的最大值及此時(shí)邊b,c的值．

19．已知a,b為兩條異面直線，α為平面，且a⊥b,a⊥α，b?α．（1）若直線c∥a,通過(guò)直線與平面垂直的判定定理，證明：c⊥α；（2）用反證法證明：b∥α．

21．在等差數(shù)列{an}中，Sn為其前n項(xiàng)和（n∈N+）．若a2=3，S4=16．（1）求數(shù)列{an}的通項(xiàng)公式；（2）設(shè)bn=1an?an+1，求數(shù)列{bn}的前n項(xiàng)和Tn．

1．給出下列四個(gè)命題，其中正確的命題是（　　）
①平行于同一直線的兩條直線平行；
②平行于同一平面的兩條直線平行；
③平行于同一直線的兩個(gè)平面平行；
④平行于同一平面的兩個(gè)平面平行．

2．已知角α的終邊經(jīng)過(guò)點(diǎn)P（-3，-4），則
cos
（
3
2
π
-
α
）
的值等于（　　）

3．在△ABC中，a=2，
B
=
π
3
，△ABC的面積等于
3
2
，則b等于（　　）

5．已知1≤a≤4，-1≤b≤2，則3a-b的取值范圍是（　　）

6．已知f（x）=2sin3x,則下列說(shuō)法正確的是（　　）

7．已知
a
，
b
是單位向量，且
2
a
+
b
=
（

-
3

，

1

）
，則
|

a
-
b

|
=（　　）

8．不等式-2x²+x+3≤0的解集是（　　）

9．已知等差數(shù)列{a_n}的前n項(xiàng)和為S_n，若S₉=54，S₈-S₅=30，則S₁₁=（　　）

10．已知數(shù)列{a_n}滿足a₁=1，a_n+1=2a_n，則a₄=（　　）

11．若一個(gè)幾何體的三視圖如圖所示，則該幾何體的體積為（　　）

14．已知函數(shù)f（x）是定義在R上的奇函數(shù)，且當(dāng)x＞0時(shí)，f（x）=cos3x+sin2x,則當(dāng)x＜0時(shí)，f（x）的表達(dá)為
．

15．△ABC?的外心為O?，三個(gè)內(nèi)角A，B，C?所對(duì)的邊分別為
a
,
b
,
c
,
AO
?
BC
=
1
2
a
（
a
-
8
5
c
）
?，b=4?．則△ABC?面積的最大值為
．

16．若x＞1，則x+
1
x
-
1
的最小值是
．

17．已知向量
a
，
b
滿足
|
a
|
=
1
，
|
b
|
=
2
，
（
2
a
-
b
）
?
（
a
+
2
b
）
=
1
．
（1）求
a
與
b
的夾角θ；
（2）求
|
a
-
2
b
|
的值．

18．在△ABC中，角A，B，C的對(duì)邊分別為a,b,c,且
tan
A
tan
B
=
2
c
-
b
b
．
（Ⅰ）求角A的大小；
（Ⅱ）若a=2，求△ABC面積的最大值及此時(shí)邊b,c的值．

19．已知a,b為兩條異面直線，α為平面，且a⊥b,a⊥α，b?α．
（1）若直線c∥a,通過(guò)直線與平面垂直的判定定理，證明：c⊥α；
（2）用反證法證明：b∥α．

21．在等差數(shù)列{a_n}中，S_n為其前n項(xiàng)和（n∈N₊）．若a₂=3，S₄=16．
（1）求數(shù)列{a_n}的通項(xiàng)公式；
（2）設(shè)
b
n
=
1
a
n
?
a
n
+
1
，求數(shù)列{b_n}的前n項(xiàng)和T_n．