當前位置：試卷中心 > 試卷詳情

2024-2025學年廣東省東莞第四高級中學高三（下）月考數學試卷（2月份）

發布：2025/6/29 9:0:20

一、選擇題：本題共8小題，每小題5分，共40分。在每小題給出的四個選項中，只有?一項是符合題目要求的。

1．在空間中，下列命題正確的是（　　）

A．若平面α內有無數條直線與直線l平行，則l∥α

B．若平面α內有無數條直線與平面β平行，則α∥β

C．若平面α內有無數條直線與直線l垂直，則l⊥α

D．若平面α內有無數條直線與平面β垂直，則α⊥β

組卷：93引用：3難度：0.7

解析

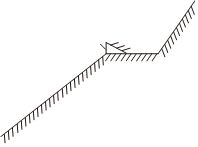2．2022北京冬奧會順利召開，滑雪健將谷愛凌以2金1銀的優秀成績書寫了自己的傳奇，現在她從某斜坡上滑下，滑過一高度不計的滑板后落在另一斜坡上，若滑板與水平地面夾角的正切值為
2
3
，斜坡與水平地面夾角的正切值為
4
3
，那么她最后落在斜坡上速度與水平地面夾角的正切值為（　　）（不計空氣阻力和摩擦力）
A．3 B．
10
3
C．
11
3
D．4
組卷：13引用：2難度：0.5
解析
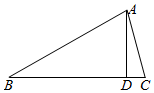3．如圖，在△ABC中，AB=BC=4，∠ABC=30°，AD是邊BC上的高，則
AD
?
AC
的值等于（　　）
A．2 B．4 C．6 D．8
組卷：338引用：7難度：0.7
解析
4．已知x,y滿足
3
x
-
a
=
0
3
x
2
+
2
y
2
+
2
a
=
0
，則x²+y²的取值范圍是（　　）
A．
[
-
9
4
，
9
2
]
B．
[
0
，
9
2
]
C．
[
-
9
4
，
0
]
D．[0，4]
組卷：46引用：1難度：0.4
解析
5．現有甲、乙兩組數據，每組數據均由8個數組成，其中甲組數據的平均數為3，方差為5，乙組數據的平均數為7，方差為1．若將這兩組數據混合成一組，則新的一組數據的方差為（　　）
A．5 B．6 C．7 D．8
組卷：122引用：4難度：0.8
解析
6．已知向量
a
=
（
6
，-
8
）
，
b
=
（
3
，
m
）
，
a
∥
b
，則
a
?
b
=（　　）
A．14 B．-14 C．50 D．-50
組卷：39引用：2難度：0.8
解析
7．已知集合A={x∈Z|x²+x-2≤0}，B={x∈N|0≤log₂（x+1）≤2}，則A∩B的真子集個數為（　　）
A．2 B．3 C．4 D．5
組卷：24引用：4難度：0.8
解析
8．i為虛數單位，復數z滿足z（1+i）=i,則|z|=（　　）
A．
1
2
B．
2
2
C．1 D．
2
組卷：108引用：7難度：0.7
解析

二、選擇題：本題共3小題，每小題6分，共18分。在每小題給出的選項中，有多項符合題目要求。全部選對的得6分，部分選對的得部分分，有選錯的得0分。

9．設平面內到定點F（0，1）和定直線l：y=-1的距離之和等于4的動點的軌跡為曲線C．關于曲線C的幾何性質，給出下列四個結論；其中所有正確結論有（　　）
A．曲線C的方程為x²=4y
B．曲線C關于y軸對稱
C．若點P（x,y）在曲線C上，則|y|≤2
D．若點P在曲線C上，則1≤|PF|≤4
組卷：9引用：1難度：0.6
解析
10．已知函數f（x）=sin（2x+φ）（-π＜φ＜0），將函數f（x）圖象向左平移
π
3
個單位長度后所得的函數圖象過點P（0，1），則函數f（x）=sin（2x+φ）（　　）
A．在區間[
π
6
，
π
3
]上單調遞減
B．在區間[
π
6
，
π
3
]上單調遞增
C．在區間[
-
π
3
，
π
6
]上單調遞減
D．在區間[-
5
π
6
，-
2
π
3
]上單調遞增
組卷：155引用：5難度：0.8
解析

11．已知圓C：x²+y²=4，直線l：（3+m）x+4y-3+3m=0，（m∈R），則下列結論正確的是（　　）

A．直線l恒過定點（3，3）

B．當m=0時，圓C上有且僅有三個點到直線l的距離都等于1

C．圓C與曲線x²+y²-6x-8y+m=0恰有三條公切線，則m=16

D．當m=13時，直線l上一個動點P向圓C引兩條切線PA，PB，其中A，B為切點，則直線AB經過點（-

，-

）

組卷：330引用：7難度：0.4

解析

三、填空題：本題共3小題，每小題5分，共15分。

12．某學校有8個社團，甲、乙兩位同學各自參加其中一個社團，且他倆參加各個社團的可能性相同，則這兩位同學參加同一個社團的概率為
．
組卷：58引用：4難度：0.9
解析
13．已知F₁，F₂分別為雙曲線
x
2
2
-
y
2
6
=
1
的左、右焦點，過F₂的直線與雙曲線的右支交于A，B兩點（其中點A位于第一象限），圓C與△AF₁F₂內切，半徑為r,則r的取值范圍是
．
組卷：281引用：4難度：0.4
解析
14．已知tan（x+
π
4
）=2，則tanx的值為
．
組卷：237引用：14難度：0.8
解析

四、解答題：本題共5小題，共77分。解答應寫出文字說明、證明過程或演算步驟。

15．已知函數f（x）=xe^x+1，g（x）=lnx+x.
（1）當a＞0時，討論函數F（x）=f（x）-1-ag（x）的零點個數；
（2）當
x
≥
1
e
2
時，證明：
f
（
x
）
[
g
（
x
）
-
1
]
+
3
＞
-
3
e
2
．
組卷：19引用：2難度：0.4
解析
16．已知△ABC內角A，B，C的對邊分別為a,b,c,且3a+2b=3ccosB．
（1）求cosC的值；
（2）若
c
=
31
，
a
+
b
=
6
，求△ABC的面積．
組卷：111引用：2難度：0.5
解析
17．已知數列{a_n}的前n項和公式為S_n=2a_n-2（n∈N^*），b_n=2log₂a_n．
（1）求證：數列{a_n}是等比數列；
（2）令c_n=a_n+（-1）ⁿb_n，求數列{c_n}的前n項和T_n．
組卷：79引用：2難度：0.5
解析
18．已知函數f（x）=ax²+x+1（a＞0）．
（1）若關于x的不等式f（x）＜0的解集為（-3，b），求f（x）的零點；
（2）若函數f（a^x）在x∈[-1，1]的最大值是11，求實數a的值；
（3）定義：區間[x₁，x₂]（x₁＜x₂）的長度為x₂-x₁．若在任意的長度為1的區間上，存在兩點函數值之差的絕對值不小于1，求實數a的最小值．
組卷：257引用：2難度：0.3
解析
19．已知中心在原點，焦點在坐標軸上的橢圓Ω，它的離心率為
1
2
，一個焦點和拋物線y²=-4x的焦點重合，過直線l：x=4上一點M引橢圓Ω的兩條切線，切點分別是A，B．
（Ⅰ）求橢圓Ω的方程；
（Ⅱ）若在橢圓
x
2
a
2
+
y
2
b
2
=
1
（
a
＞
b
＞
0
）
上的點（x₀，y₀）處的橢圓的切線方程是
x
0
x
a
2
+
y
0
y
b
2
=1．求證：直線AB恒過定點C；并求出定點C的坐標．
組卷：83引用：1難度：0.1
解析

0/60 進入組卷

0/20 進入試卷籃

布置作業 發布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

2024-2025學年廣東省東莞第四高級中學高三（下）月考數學試卷（2月份）

一、選擇題：本題共8小題，每小題5分，共40分。在每小題給出的四個選項中，只有?一項是符合題目要求的。

1．在空間中，下列命題正確的是（ ）

3．如圖，在△ABC中，AB=BC=4，∠ABC=30°，AD是邊BC上的高，則AD?AC的值等于（ ）

4．已知x,y滿足3x-a=03x2+2y2+2a=0，則x2+y2的取值范圍是（ ）

5．現有甲、乙兩組數據，每組數據均由8個數組成，其中甲組數據的平均數為3，方差為5，乙組數據的平均數為7，方差為1．若將這兩組數據混合成一組，則新的一組數據的方差為（ ）

6．已知向量a=（6，-8），b=（3，m），a∥b，則a?b=（ ）

7．已知集合A={x∈Z|x2+x-2≤0}，B={x∈N|0≤log2（x+1）≤2}，則A∩B的真子集個數為（ ）

8．i為虛數單位，復數z滿足z（1+i）=i,則|z|=（ ）

二、選擇題：本題共3小題，每小題6分，共18分。在每小題給出的選項中，有多項符合題目要求。全部選對的得6分，部分選對的得部分分，有選錯的得0分。

9．設平面內到定點F（0，1）和定直線l：y=-1的距離之和等于4的動點的軌跡為曲線C．關于曲線C的幾何性質，給出下列四個結論；其中所有正確結論有（ ）

10．已知函數f（x）=sin（2x+φ）（-π＜φ＜0），將函數f（x）圖象向左平移π3個單位長度后所得的函數圖象過點P（0，1），則函數f（x）=sin（2x+φ）（ ）

11．已知圓C：x2+y2=4，直線l：（3+m）x+4y-3+3m=0，（m∈R），則下列結論正確的是（ ）

三、填空題：本題共3小題，每小題5分，共15分。

12．某學校有8個社團，甲、乙兩位同學各自參加其中一個社團，且他倆參加各個社團的可能性相同，則這兩位同學參加同一個社團的概率為．

13．已知F1，F2分別為雙曲線x22-y26=1的左、右焦點，過F2的直線與雙曲線的右支交于A，B兩點（其中點A位于第一象限），圓C與△AF1F2內切，半徑為r,則r的取值范圍是 ．

14．已知tan（x+π4）=2，則tanx的值為．

四、解答題：本題共5小題，共77分。解答應寫出文字說明、證明過程或演算步驟。

15．已知函數f（x）=xex+1，g（x）=lnx+x.（1）當a＞0時，討論函數F（x）=f（x）-1-ag（x）的零點個數；（2）當x≥1e2時，證明：f（x）[g（x）-1]+3＞-3e2．

16．已知△ABC內角A，B，C的對邊分別為a,b,c,且3a+2b=3ccosB．（1）求cosC的值；（2）若c=31，a+b=6，求△ABC的面積．

17．已知數列{an}的前n項和公式為Sn=2an-2（n∈N*），bn=2log2an．（1）求證：數列{an}是等比數列；（2）令cn=an+（-1）nbn，求數列{cn}的前n項和Tn．

1．在空間中，下列命題正確的是（　　）

3．如圖，在△ABC中，AB=BC=4，∠ABC=30°，AD是邊BC上的高，則
AD
?
AC
的值等于（　　）

4．已知x,y滿足
3
x
-
a
=
0
3
x
2
+
2
y
2
+
2
a
=
0
，則x²+y²的取值范圍是（　　）

5．現有甲、乙兩組數據，每組數據均由8個數組成，其中甲組數據的平均數為3，方差為5，乙組數據的平均數為7，方差為1．若將這兩組數據混合成一組，則新的一組數據的方差為（　　）

6．已知向量
a
=
（
6
，-
8
）
，
b
=
（
3
，
m
）
，
a
∥
b
，則
a
?
b
=（　　）

7．已知集合A={x∈Z|x²+x-2≤0}，B={x∈N|0≤log₂（x+1）≤2}，則A∩B的真子集個數為（　　）

8．i為虛數單位，復數z滿足z（1+i）=i,則|z|=（　　）

9．設平面內到定點F（0，1）和定直線l：y=-1的距離之和等于4的動點的軌跡為曲線C．關于曲線C的幾何性質，給出下列四個結論；其中所有正確結論有（　　）

10．已知函數f（x）=sin（2x+φ）（-π＜φ＜0），將函數f（x）圖象向左平移
π
3
個單位長度后所得的函數圖象過點P（0，1），則函數f（x）=sin（2x+φ）（　　）

11．已知圓C：x²+y²=4，直線l：（3+m）x+4y-3+3m=0，（m∈R），則下列結論正確的是（　　）

12．某學校有8個社團，甲、乙兩位同學各自參加其中一個社團，且他倆參加各個社團的可能性相同，則這兩位同學參加同一個社團的概率為
．

13．已知F₁，F₂分別為雙曲線
x
2
2
-
y
2
6
=
1
的左、右焦點，過F₂的直線與雙曲線的右支交于A，B兩點（其中點A位于第一象限），圓C與△AF₁F₂內切，半徑為r,則r的取值范圍是
．

14．已知tan（x+
π
4
）=2，則tanx的值為
．

15．已知函數f（x）=xe^x+1，g（x）=lnx+x.
（1）當a＞0時，討論函數F（x）=f（x）-1-ag（x）的零點個數；
（2）當
x
≥
1
e
2
時，證明：
f
（
x
）
[
g
（
x
）
-
1
]
+
3
＞
-
3
e
2
．

16．已知△ABC內角A，B，C的對邊分別為a,b,c,且3a+2b=3ccosB．
（1）求cosC的值；
（2）若
c
=
31
，
a
+
b
=
6
，求△ABC的面積．

17．已知數列{a_n}的前n項和公式為S_n=2a_n-2（n∈N^*），b_n=2log₂a_n．
（1）求證：數列{a_n}是等比數列；
（2）令c_n=a_n+（-1）ⁿb_n，求數列{c_n}的前n項和T_n．