2022-2023學年黑龍江省哈爾濱一中高三(上)期中數學試卷
發布:2025/6/29 10:0:14
一、單項選擇題:(本題共8小題,每小題5分,共40分。在每小題給出的四個選項中,只有一項符合題目要求)
-
1.已知a>b>0,c>d>0,下列判斷中正確的是( )
A.a-c<b-d B.ac>bd C. <adbcD.ad>bc 組卷:17引用:4難度:0.9 -
2.已知
,則a,b,c的大小關系為( )a=log78,b=87,c=log89A.a>b>c B.c>b>a C.a>c>b D.b>a>c 組卷:12引用:1難度:0.6 -
3.在復平面內,復數1-2i與-1+3i分別對應向量
和ON,其中O為坐標原點,則OM=( )|NM|A.1 B.5 C. 2D. 29組卷:19引用:2難度:0.8 -
4.某車間分批生產某種產品,每批的生產準備費用為900元,若每批生產x件,則平均倉儲時間為
天,且每件產品每天的倉儲費用為1元,為使平均到每件產品的生產準備費用與倉儲費用之和最小,每批應生產產品( )x4A.30件 B.60件 C.80件 D.100件 組卷:122引用:4難度:0.8 -
5.設集合A={x|-2≤x≤5},B={x|m+1≤x≤2m-1},則A∩B=B,則實數m的取值范圍是( )
A.[2,3] B.(-∞,3] C.(2,3] D.(-∞,2] 組卷:93引用:5難度:0.9 -
6.已知數列{an}滿足
,則下列結論中錯誤的個數為( )a1=m(m>0),an+1=an-1,an>11an,0<an≤1
①若a3=4,則m可以取3個不同的值;
②若,則數列{an}是周期為3的數列;m=2
③對于任意的T∈N*且T≥2,存在m>1,使得{an}是周期為T的數列;
④存在m∈Q且m≥2,使得數列{an}是周期數列.A.4 B.3 C.2 D.1 組卷:74引用:1難度:0.5 -
7.已知空間兩不同直線m,n,兩不同平面α,β,下列命題正確的是( )
A.若m∥α且n∥α,則m∥n B.若m⊥β且m∥n,則n∥β C.若m⊥α且m∥β,則α⊥β D.若m不垂直于α,且n?α,則m不垂直于n 組卷:206引用:5難度:0.6 -
8.已知
,則cosθ=23=( )sin(2θ+π2)A. -19B. 19C. -89D. 89組卷:459引用:2難度:0.8
二、多項選擇題:(本題共4小題,每小題5分,共20分。在每小題給出的選項中,有多項符合題目要求。全部選對的得5分,有選錯的得0分,部分選對的得2分)
-
9.已知直四棱柱
,底面ABCD是邊長為4的菱形,且∠BAD=120°,點E,F,G,H分別為A1B1,A1D1,DD1,BC的中點.以A1為球心作半徑為R的球,下列說法正確的是( )ABCD-A1B1C1D1,AA1=43A.點E,F,G,H四點共面 B.直線BE與直線AF所成角的余弦值為 2526C.當球與直四棱柱的五個面有交線時,R的范圍是 (23,4)D.在直四棱柱內,球A1外放置一個小球,當小球的體積最大時,球A1半徑的最大值為 31-3組卷:61引用:3難度:0.4 -
10.函數f(x)=sin(2x+φ)的圖像向左平移
個單位后得到一個偶函數的圖像,則φ的值可以為( )π8A.0 B. π4C. -3π4D. -π4組卷:17引用:1難度:0.7 -
11.已知向量
=(2,1),a=(-3,1),則下列說法正確的是( )bA.( +a)⊥baB.| +2a|=5bC.向量 在向量a方向上的投影的數量是b102D.與向量 方向相同的單位向量是a(255,55)組卷:203引用:6難度:0.6 -
12.已知函數y=f(x)滿足:對于任意實數x,y∈R,都有f(x+y)+f(x-y)=2f(x)cosy,且f(0)=0,則( )
A.f(x)是奇函數 B.f(x)是周期函數 C.?x∈R,|f(x)|≤1 D.f(x)在[- ,π2]上是增函數π2組卷:52引用:2難度:0.6
三、填空題:(本題共4小題,每小題5分,共20分)
-
13.已知函數f(x)=x3.設曲線y=f(x)在點P(x1,f(x1))處的切線與該曲線交于另一點Q(x2,f(x2)),記f'(x)為函數f(x)的導數,則
的值為.f′(x1)f′(x2)組卷:189引用:5難度:0.5 -
14.設函數f(x)=
,則f(-3)+f(log23)=.log2(1-x),x<04x,x≥0組卷:244引用:10難度:0.9 -
15.圓柱的側面展開圖是邊長為2π和3π的矩形,則圓柱的體積為
.組卷:53引用:3難度:0.7 -
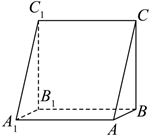 16.中國古代數學著作《九章算術》中,將底面是直角三角形的直三棱柱稱之為“塹堵”.在如圖所示的塹堵ABC-A1B1C1中,AA1=AC=5,AB=3,BC=4,則塹堵ABC-A1B1C1的外接球的體積是 .組卷:23引用:3難度:0.6
16.中國古代數學著作《九章算術》中,將底面是直角三角形的直三棱柱稱之為“塹堵”.在如圖所示的塹堵ABC-A1B1C1中,AA1=AC=5,AB=3,BC=4,則塹堵ABC-A1B1C1的外接球的體積是 .組卷:23引用:3難度:0.6
四、解答題:(本題共6小題,共70分。解答應寫出文字說明、證明過程或演算步驟。)
-
17.已知數列{an}是首項為2的等差數列,數列{bn}是公比為2的等比數列,且數列{an?bn}的前n項和為
.Sn=n?2n+1(n∈N*)
(1)求數列{an},{bn}的通項公式;
(2)設_____,求數列{cn}的前n項和為Tn.
①,②cn=anbn,③cn=an+bn.從這三個條件中任選一個填入上面橫線中,并回答問題.cn=1an?log2bn組卷:19引用:3難度:0.5 -
 18.如圖,在△ABC中,AD是BC邊上的高,以AD為折痕,將△ACD折至△APD的位置,使得PB⊥AB.
18.如圖,在△ABC中,AD是BC邊上的高,以AD為折痕,將△ACD折至△APD的位置,使得PB⊥AB.
(1)證明:PB⊥平面ABD;
(2)若AD=PB=4,BD=2,求二面角B-PA-D的正弦值.組卷:953引用:12難度:0.5 -
 19.如圖,在△ABC中,B=,D是BC邊上一點,AD=4π6,CD=7,AC=5.2
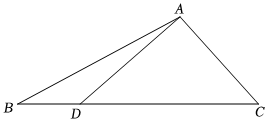
19.如圖,在△ABC中,B=,D是BC邊上一點,AD=4π6,CD=7,AC=5.2
(1)求∠ADC的大小;
(2)求AB的長.組卷:99引用:2難度:0.7 -
20.已知Sn為數列{an}的前n項和,a1=1,
.Sn+1+Sn=2n2+2n+1
(1)求{an}的通項公式;
(2)若b1=1,,求數列{bn}的前n項和Tn.bn+1+(-1)nbn=an組卷:201引用:4難度:0.5 -
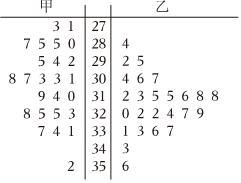 21.從甲、乙兩品種的棉花中各抽測了25根棉花的纖維長度(單位:mm),得到如圖5的莖葉圖,整數位為莖,小數位為葉,如27.1mm的莖為27,葉為1.
21.從甲、乙兩品種的棉花中各抽測了25根棉花的纖維長度(單位:mm),得到如圖5的莖葉圖,整數位為莖,小數位為葉,如27.1mm的莖為27,葉為1.
(Ⅰ)試比較甲、乙兩種棉花的纖維長度的平均值的大小及方差的大小;(只需寫出估計的結論,不需說明理由)
(Ⅱ)將棉花按纖維長度的長短分成七個等級,分級標準如表:
試分別估計甲、乙兩種棉花纖維長度等級為二級的概率;等級 七 六 五 四 三 二 一 長度(mm) 小于26.0 [26.0,27.0) [27.0,28.0) [28.0,29.0) [29.0,30.0) [30.0,31.0) 不小于31.0
(Ⅲ)為進一步檢驗甲種棉花的其它質量指標,現從甲種棉花中隨機抽取4根,記ξ為抽取的棉花纖維長度為二級的根數,求ξ的分布列和數學期望.組卷:54引用:2難度:0.7 -
22.已知函數f(x)=eax-2ax(a∈R,a≠0).
(1)討論f(x)的單調性;
(2)若不等式f(x)≥sinx-cosx+2-2ax對任意x≥0恒成立,求實數a的取值范圍.組卷:71引用:2難度:0.5


