當前位置：試卷中心 > 試卷詳情

2019-2020學年黑龍江省牡丹江第三高級中學高一（上）期中數學試卷

發布：2025/6/29 14:0:13

一、選擇題：本題共12小題，每小題5分，共60分．在每小題給出的四個選項中，只有一項是符合題目要求的。

1．已知集合A={x∈Q|（x-1）（x²-2）=0}，B={x∈R|（x-1）（x²-2）=0}，則下列關系正確的是（　　）
A．A=B B．A?B C．B?A D．A∩B=?
組卷：105引用：2難度：0.7
解析
2．已知
A
=
{
x
|
lo
g
2
1
x
＜
2
）
，B={x|x²-x-2≤0}，則（?_RA）∩B=（　　）
A．
{
x
|
-
1
≤
x
≤
1
4
}
B．
|
x
|
-
2
≤
x
≤
1
4
}
C．R D．
{
x
|
x
≥
1
4
}
組卷：56引用：1難度：0.7
解析
3．當a＞1時，在同一坐標系中，函數y=a^x與y=log_ax的圖象是（　　）
A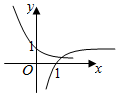． B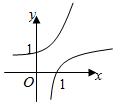． C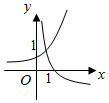． D．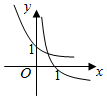
組卷：1484引用：7難度：0.9
解析
4．若函數
y
=
（
2
+
x
）
（
m
-
x
）
為偶函數，則m=（　　）
A．-2 B．2 C．
-
2
D．
2
組卷：466引用：2難度：0.9
解析
5．若函數f（x）=
x
+
3
+
1
x
+
2
，則f（1）=（　　）
A．1 B．
5
3
C．
7
3
D．
13
3
組卷：22引用：3難度：0.8
解析
6．函數
y
=
lo
g
1
2
（
2
-
x
-
x
2
）
的增區間為（　　）
A．
（
-
∞
，-
1
2
）
B．
（
-
2
，-
1
2
）
C．
（
-
1
2
，
+
∞
）
D．
（
-
1
2
，
1
）
組卷：364引用：11難度：0.7
解析
7．函數
f
（
x
）
=
x
+
1
x
-
1
的定義域是（　　）
A．（-∞，-1）∪（1，+∞） B．[-1，+∞）
C．[-1，0） D．[-1，1）∪（1，+∞）
組卷：28引用：1難度：0.8
解析
8．我國著名數學家華羅庚先生曾說：“數缺形時少直觀，形缺數時難入微，數形結合百般好，隔裂分家萬事休．”在數學的學習和研究中，常用函數的圖象來研究函數的性質，也常用函數的解析式來分析函數圖象的特征，函數f（x）=（x+
1
x
）ln|
1
x
|的圖象大致為（　　）
A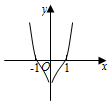． B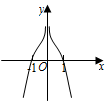． C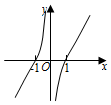． D．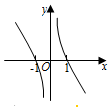
組卷：197引用：4難度：0.9
解析
9．正整數1，2，3，…，n的倒數的和1+
1
2
+
1
3
+
?
+
1
n
已經被研究了幾百年，但是迄今為止仍然沒有得到它的求和公式，只是得到了它的近似公式；當n很大時1+
1
2
+
1
3
+
?
+
1
n
≈lnn+γ．其中γ稱為歐拉-馬歇羅尼常數，γ≈0.577215664901?，至今為止都不確定γ是有理數還是無理數．設[x]表示不超過x的最大整數．用上式計算
[
1
+
1
2
+
1
3
+
?
+
1
2022
]
的值為（　　）（參考數據：ln2≈0.69，ln3≈1.10，ln10≈2.30）
A．7 B．8 C．9 D．10
組卷：185引用：6難度：0.7
解析
10．f（x）=2^x+4x-3零點所在的區間是（　　）
A．（2，3） B．（1，2） C．（0，1） D．（-1，0）
組卷：99引用：2難度：0.7
解析
11．已知
a
=
（
2
）
4
3
，
b
=
2
2
5
，
c
=
9
1
3
，則（　　）
A．b＜a＜c B．a＜b＜c C．b＜c＜a D．c＜a＜b
組卷：962引用：4難度：0.7
解析
12．若冪函數y=f（x）的圖象過點
（
8
，
2
2
）
，則函數f（x-1）-f²（x）的最大值為（　　）
A．
1
2
B．
-
1
2
C．
-
3
4
D．-1
組卷：208引用：4難度：0.7
解析

二、填空題：本題共4小題，每小題5分，共20分．

13．若{a,b,c}?{-3，-2，-1，0，1，2，3，4}，則符合條件的二次函數y=ax²+bx+c的解析式有
個．
組卷：9引用：2難度：0.7
解析
14．不等式（
1
3
）^x-1≤9的解集為
．
組卷：99引用：2難度：0.7
解析
15．函數
f
（
x
）
=
x
-
1
2
的定義域為
，值域為
．
組卷：11引用：1難度：0.8
解析
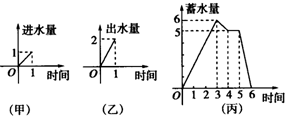16．水池有兩個相同的進水口和一個出水口，每個口進出水速度如圖（甲）、（乙）所示，某天0點到6點該水池蓄水量如圖（丙）所以（至少打開一個水口）給出以下3個論斷：
①0點到3點只進水不出水；
②3點到4點不進水只出水；
③4點到5點不進水也不出水．
則一定正確的論斷是
．
組卷：39引用：1難度：0.7
解析

三、解答題：共70分。解答應寫出文字說明、證明過程或演算步驟。

17．若函數f（x）滿足：對于任意正數s,t,都有f（s）＞0，f（t）＞0，且f（s）+f（t）＜f（s+t），則稱函數
f（x）為“L函數”．
（1）試判斷函數h（x）=x²是否是“L函數”，并說明理由；
（2）若函數g（x）=3^x-1+a（3^-x-1）為“L函數”，求實數a的取值范圍；
（3）若函數f（x）為“L函數”，且f（1）=1，
求證：對任意x∈（2^k-1，2^k）（k∈N^*），都有
f
（
x
）
＞
x
2
．
組卷：51引用：2難度：0.4
解析
18．計算下面各題
（1）lg25-lg
1
4
+9^lg1+log₂（log₂16）．
（2）log_2.56.25+lg
1
100
+ln（e
e
）．
組卷：117引用：1難度：0.8
解析
19．已知二次函數f（x）=x²-16x+p+3．
（1）若函數在區間[-1，1]上存在零點，求實數p的取值范圍；
（2）問是否存在常數q（q≥0），當x∈[q,10]時，f（x）的值域為區間D，且D的長度為12-q.（注：區間[a,b]（a＜b）的長度為b-a）．
組卷：730引用：9難度：0.1
解析
20．設集合A={x|-1≤x≤2}，集合B={x|2m＜x＜1-m}．
（1）若“?x∈R，x∈（A∩B）”為假命題，求實數m的取值范圍；
（2）若A∩B中有只有三個整數，求實數m的取值范圍．
組卷：32引用：1難度：0.7
解析
21．已知函數f（x）=log_a（x+1），g（x）=log_a（4-2x）（a＞0，且a≠1）．
（1）求函數f（x）-g（x）的定義域；
（2）求使函數f（x）-g（x）的值為正數的x的取值范圍．
組卷：216引用：19難度：0.3
解析
22．已知f（x）=x|x-a|+2x-3．
（Ⅰ）當a=4，2≤x≤5時，問x分別取何值時，函數f（x）取得最大值和最小值，并求出相應的最大值和最小值；
（Ⅱ）若f（x）在R上恒為增函數，試求a的取值范圍．
組卷：25引用：1難度：0.5
解析

0/60 進入組卷

0/20 進入試卷籃

布置作業 發布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

A．（-∞，-1）∪（1，+∞）	B．[-1，+∞）
C．[-1，0）	D．[-1，1）∪（1，+∞）

2019-2020學年黑龍江省牡丹江第三高級中學高一（上）期中數學試卷

一、選擇題：本題共12小題，每小題5分，共60分．在每小題給出的四個選項中，只有一項是符合題目要求的。

1．已知集合A={x∈Q|（x-1）（x2-2）=0}，B={x∈R|（x-1）（x2-2）=0}，則下列關系正確的是（ ）

2．已知A={x|log21x＜2），B={x|x2-x-2≤0}，則（?RA）∩B=（ ）

3．當a＞1時，在同一坐標系中，函數y=ax與y=logax的圖象是（ ）

4．若函數y=（2+x）（m-x）為偶函數，則m=（ ）

5．若函數f（x）=x+3+1x+2，則f（1）=（ ）

6．函數y=log12（2-x-x2）的增區間為（ ）

7．函數f（x）=x+1x-1的定義域是（ ）

10．f（x）=2x+4x-3零點所在的區間是（ ）

11．已知a=（2）43，b=225，c=913，則（ ）

12．若冪函數y=f（x）的圖象過點（8，22），則函數f（x-1）-f2（x）的最大值為（ ）

二、填空題：本題共4小題，每小題5分，共20分．

13．若{a,b,c}?{-3，-2，-1，0，1，2，3，4}，則符合條件的二次函數y=ax2+bx+c的解析式有 個．

14．不等式（13）x-1≤9的解集為 ．

15．函數f（x）=x-12的定義域為 ，值域為．

三、解答題：共70分。解答應寫出文字說明、證明過程或演算步驟。

18．計算下面各題（1）lg25-lg14+9lg1+log2（log216）．（2）log2.56.25+lg1100+ln（ee）．

19．已知二次函數f（x）=x2-16x+p+3．（1）若函數在區間[-1，1]上存在零點，求實數p的取值范圍；（2）問是否存在常數q（q≥0），當x∈[q,10]時，f（x）的值域為區間D，且D的長度為12-q.（注：區間[a,b]（a＜b）的長度為b-a）．

20．設集合A={x|-1≤x≤2}，集合B={x|2m＜x＜1-m}．（1）若“?x∈R，x∈（A∩B）”為假命題，求實數m的取值范圍；（2）若A∩B中有只有三個整數，求實數m的取值范圍．

21．已知函數f（x）=loga（x+1），g（x）=loga（4-2x）（a＞0，且a≠1）．（1）求函數f（x）-g（x）的定義域；（2）求使函數f（x）-g（x）的值為正數的x的取值范圍．

22．已知f（x）=x|x-a|+2x-3．（Ⅰ）當a=4，2≤x≤5時，問x分別取何值時，函數f（x）取得最大值和最小值，并求出相應的最大值和最小值；（Ⅱ）若f（x）在R上恒為增函數，試求a的取值范圍．

1．已知集合A={x∈Q|（x-1）（x²-2）=0}，B={x∈R|（x-1）（x²-2）=0}，則下列關系正確的是（　　）

2．已知
A
=
{
x
|
lo
g
2
1
x
＜
2
）
，B={x|x²-x-2≤0}，則（?_RA）∩B=（　　）

3．當a＞1時，在同一坐標系中，函數y=a^x與y=log_ax的圖象是（　　）

4．若函數
y
=
（
2
+
x
）
（
m
-
x
）
為偶函數，則m=（　　）

5．若函數f（x）=
x
+
3
+
1
x
+
2
，則f（1）=（　　）

6．函數
y
=
lo
g
1
2
（
2
-
x
-
x
2
）
的增區間為（　　）

7．函數
f
（
x
）
=
x
+
1
x
-
1
的定義域是（　　）

10．f（x）=2^x+4x-3零點所在的區間是（　　）

11．已知
a
=
（
2
）
4
3
，
b
=
2
2
5
，
c
=
9
1
3
，則（　　）

12．若冪函數y=f（x）的圖象過點
（
8
，
2
2
）
，則函數f（x-1）-f²（x）的最大值為（　　）

13．若{a,b,c}?{-3，-2，-1，0，1，2，3，4}，則符合條件的二次函數y=ax²+bx+c的解析式有
個．

14．不等式（
1
3
）^x-1≤9的解集為
．

15．函數
f
（
x
）
=
x
-
1
2
的定義域為
，值域為
．

18．計算下面各題
（1）lg25-lg
1
4
+9^lg1+log₂（log₂16）．
（2）log_2.56.25+lg
1
100
+ln（e
e
）．

19．已知二次函數f（x）=x²-16x+p+3．
（1）若函數在區間[-1，1]上存在零點，求實數p的取值范圍；
（2）問是否存在常數q（q≥0），當x∈[q,10]時，f（x）的值域為區間D，且D的長度為12-q.（注：區間[a,b]（a＜b）的長度為b-a）．

20．設集合A={x|-1≤x≤2}，集合B={x|2m＜x＜1-m}．
（1）若“?x∈R，x∈（A∩B）”為假命題，求實數m的取值范圍；
（2）若A∩B中有只有三個整數，求實數m的取值范圍．

21．已知函數f（x）=log_a（x+1），g（x）=log_a（4-2x）（a＞0，且a≠1）．
（1）求函數f（x）-g（x）的定義域；
（2）求使函數f（x）-g（x）的值為正數的x的取值范圍．

22．已知f（x）=x|x-a|+2x-3．
（Ⅰ）當a=4，2≤x≤5時，問x分別取何值時，函數f（x）取得最大值和最小值，并求出相應的最大值和最小值；
（Ⅱ）若f（x）在R上恒為增函數，試求a的取值范圍．