2021年江西省新余市高考數學二模試卷（理科）

一、選擇題（本大題共12小題，每小題5分，共60分.在每小題給出的四個選項中，只有一項是符合題目要求的.）

• 1．集合A=（-2，3]，B=（1，4），則A∩B=（　　）

  A．（1，3]

  B．（-2，4）

  C．（-2，1）

  D．（3，4）
  組卷：4引用：2難度：0.7

  解析

• 2．已知函數f（x）=sin（ωx+φ）（ω＞0，|φ|＜

  π

  2

  ），若f（x+

  π

  6

  ）為偶函數，y=f（x）的圖象與x軸交點的橫坐標構成一個公差為

  π

  2

  的等差數列．將函數f（x）圖象上每一點的橫坐標縮短為原來的

  1

  2

  ，縱坐標不變，再向左平移

  π

  12

  個單位后得到函數g（x）的圖象．則f（

  π

  3

  ）+g（

  π

  3

  ）=（　　）

  A．0

  B．-2

  C．1

  D．-1
  組卷：145引用：2難度：0.6

  解析

• 3．一組數據按照從小到大的順序排列為1，2，3，5，6，8，記這組數據的上四分位數為n,則二項式

  （

  2

  x

  -

  1

  x

  ）

  n

  展開式的常數項為（　　）

  A．-160

  B．60

  C．120

  D．240
  組卷：294引用：5難度：0.7

  解析

• 4．若（1+i）z=-2，則z-

  z

  =（　　）

  A．-2i

  B．2i

  C．-2

  D．2
  組卷：122引用：2難度：0.8

  解析

• 5．△ABC中∠C=90°，AC=2，P為線段BC上任一點，則

  AP

  ?

  AC

  =（　　）

  A．2

  B．4

  C．8

  D．不確定
  組卷：111引用：3難度：0.8

  解析

• 6．已知橢圓的左、右焦點分別為F₁，F₂，直線AB過F₁與橢圓交于A，B兩點，若△F₂AB為正三角形，該橢圓的離心率為（　　）

  A． 1 3

  B． 1 2

  C． 3 3

  D． 6 3
  組卷：511引用：4難度：0.6

  解析

• 7．若函數y=f（x）的定義域M={x|-2≤x≤2}，值域為N={y|0≤y≤2}，則函數y=f（x）的圖象可能是（　　）

  A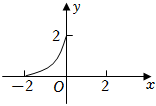．	B．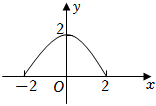
  C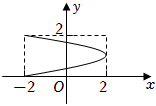．	D．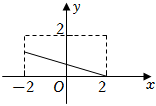
  組卷：73引用：5難度：0.9

  解析

• 8．已知雙曲線C：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  0

  ，

  b

  ＞

  0

  ）

  的左、右焦點分別為F₁，F₂，一條漸近線為l,過點F₂且與l平行的直線交雙曲線C于點M，若|MF₁|=2|MF₂|，則雙曲線C的離心率為（　　）

  A． 2

  B． 3

  C． 5

  D． 6
  組卷：441引用：7難度：0.7

  解析

• 9．設函數f（x）=|lgx|，若存在實數0＜a＜b,滿足f（a）=f（b），則M=log₂

  a

  2

  +

  b

  2

  8

  ，N=log₂（

  1

  a

  +

  b

  ）²，Q=ln

  1

  e

  2

  的關系為（　　）

  A．M＞N＞Q

  B．M＞Q＞N

  C．N＞Q＞M

  D．N＞M＞Q
  組卷：120引用：2難度：0.6

  解析

• 10．設20件產品中有5件不合格，從中任意取出2件，在所取得的產品中發現有一件不合格品，求另一件也是不合格品的概率為（　　）

  A． 1 19

  B． 17 38

  C． 4 19

  D． 2 17
  組卷：10引用：1難度：0.7

  解析
• 11．系統找不到該試題
• 12．系統找不到該試題

二、填空題（本大題共4小題，每題5分，共20分.請將正確答案填在答題卷相應位置.）

• 13．在某校舉行的數學競賽中，全體參賽學生的競賽成績近似服從正態分布N（70，100）．已知成績在80到90分之間的學生有120名，若該校計劃獎勵競賽成績在90分以上（含90分）的學生，估計獲獎的學生有

  人．（填一個整數）
  （參考數據：若X～N（μ，σ²），有P（μ-σ≤X≤μ+σ）≈0.6827，P（μ-2σ≤X≤μ+2σ）≈0.9545，P（μ-3σ≤X≤μ+3σ）≈0.9973）
  組卷：3引用：0難度：0.7

  解析

• 14．設

  f

  （

  x

  ）

  =

  2

  x

  +

  1

  x

  +

  2

  ，g（x）=（x+2）³+2，h（x）=

  （

  x

  +

  2

  ）

  1

  3

  +

  2

  ，若f（x）與g（x），h（x）的圖像的交點分別為A，B，C，D四點，O為坐標原點，則

  |

  OA

  +

  OB

  +

  OC

  +

  OD

  |

  =

  ．
  組卷：2引用：1難度：0.6

  解析

• 15．已知數列{a_n}滿足

  a

  1

  =

  1

  ，

  a

  n

  +

  1

  =

  n

  n

  +

  1

  a

  n

  （

  n

  ∈

  N

  ，

  n

  ?

  1

  ）

  ，則a_n=

  ．
  組卷：151引用：3難度：0.5

  解析

• 16．已知正四棱錐O-ABCD（底面是正方形且頂點在頂面的射影是底面正方形的中心的棱錐叫做正四棱錐）的體積為12，底面邊長為2

  3

  ，則正四棱錐O-ABCD內切球的表面積為

   

  ．
  組卷：57引用：1難度：0.7

  解析

三、解答題（本大題共5小題，共70分，解答應寫出必要的文字說明、證明過程及演算步驟）

• 17．在△ABC中，內角A，B，C的對邊分別為a,b,c,且asinA-csinC=（

  3

  a-b）sinB．
  （1）求角C的大小；
  （2）若sinA?sinB=

  3

  3

  ，c=2，求△ABC的面積．
  組卷：534引用：1難度：0.6

  解析

• 18．在平面直角坐標系xOy中，直線l的參數方程為

  x = - 1 + tcosα

  y = 1 + tsinα

  （其中α為直線的傾斜角，t為參數），在以為O極點，x軸的非負半軸為極軸的極坐標系中，曲線C的極坐標方程為ρsin²θ-4cosθ=0．
  （1）當直線l的斜率k=2時，求曲線C上的點A與直線l上的點B間的最小距離；
  （2）如果直線l與曲線C有兩個不同交點，求直線l的斜率k的取值范圍．
  組卷：77引用：2難度：0.5

  解析

• 19．已知O為坐標原點，拋物線C：y²=2px（p＞0）的焦點為F，P是C上在第一象限內的一點，PF與x軸垂直，

  |

  OP

  |

  =

  3

  5

  ．
  （1）求C的方程；
  （2）經過點F的直線l與C交于異于點P的A，B兩點，若△PAB的面積為

  18

  3

  ，求l的方程．
  組卷：104引用：5難度：0.5

  解析

• 20．某學校為了提升學生學習數學的興趣，舉行了“趣味數學”闖關比賽，每輪比賽從10道題中任意抽取3道回答，每答對一道題積1分．已知小明同學能答對10道題中的6道題．
  （1）求小明同學在一輪比賽中所得積分X的分布列和期望；
  （2）規定參賽者在一輪比賽中至少積2分才視為闖關成功，若參賽者每輪闖關成功的概率穩定且每輪是否闖關成功相互獨立，問：小明同學在5輪闖關比賽中，需幾次闖關成功才能使得對應概率取值最大？
  組卷：52引用：4難度：0.5

  解析

• 21．已知函數．f（x）=e^x（1+mlnx），其中m＞0，f′（x）為f（x）的導函數．
  （1）當m=1，求f（x）在點（1，f（1））處的切線方程；
  （2）設函數

  h

  （

  x

  ）

  =

  f

  ′

  （

  x

  ）

  e

  x

  ，且

  h

  （

  x

  ）

  ≥

  5

  2

  恒成立．
  ①求m的取值范圍；
  ②f′（x）的極小值點為x₀，求證：

  1

  2

  ＜

  x

  0

  ＜

  1

  ．
  組卷：52引用：2難度：0.2

  解析

選考題：（本小題滿分10分）.請考生在第22、23題中任選一題作答.如果多做，則按所做的第一題計分.[選修4-4：坐標系與參數方程]

• 22．已知不等式|2x+2|-|x-2|＞2的解集為M．
  （1）求集合M；
  （2）已知t為集合M中的最小正整數，若a＞1，b＞1，c＞1，且（a-1）（b-1）（c-1）=t,求證：abc≥8．
  組卷：25引用：3難度：0.4

  解析

[選修4-5：不等式選講]

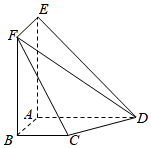• 23．如圖所示，AE⊥平面ABCD，四邊形AEFB為矩形，BC∥AD，BA⊥AD，AE=AD=2AB=2BC=4．
  （1）求證：CF∥平面ADE；
  （2）求平面CDF與平面AEFB所成銳二面角的余弦值．
  組卷：356引用：16難度：0.4

  解析