當前位置：試卷中心 > 試卷詳情

2021-2022學年陜西省西安市高新一中高二（上）期中數學試卷（理科）

發布：2025/6/29 16:0:15

一、選擇題（本大題共10個小題，每小題4分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的）

1．記等差數列{a_n}的前n項和為S_n．若a₃+a₁₃=a₉，則下列一定成立的是（　　）
A．S₆＜S₈ B．S₆＞S₈ C．S₁₃=0 D．S₁₄=0
組卷：190引用：2難度：0.6
解析

2．給出下列結論，其中不正確的是（　　）

A．若命題p：?x₀∈R，x₀²+x₀+1＜0，則￢p：?x₀∈R，x₀²+x₀+1≥0

B．“x²＜4”是“x＜2”的充分而不必要條件

C．命題“若一個數是負數，則它的平方是正數”的否命題是：“若一個數不是負數，則它的平方不是正數”

D．在一次環保知識競賽中，設命題p是“甲獲獎”，q是“乙獲獎”，則命題“至少有一人沒有獲獎”可表示為（￢p）∧（￢q）

組卷：3引用：1難度：0.7

解析

3．為了得到函數y=cos（3x-1）的圖象，只需把y=cos3x的圖象上的所有點（　　）
A．向左平移1個單位 B．向右平移1個單位
C．向左平移
1
3
個單位 D．向右平移
1
3
個單位
組卷：293引用：3難度：0.7
解析
4．已知向量
a
，
b
滿足|
a
|=1，|
b
|=2，且
a
與
b
的夾角為
π
3
，則向量
a
-
b
與
b
的夾角為（　　）
A．
π
6
B．
π
3
C．
2
π
3
D．
5
π
6
組卷：344引用：3難度：0.7
解析
5．設集合U={x∈N|0＜x≤8}，S={1，2，3，4，5}，T={3，5，7}，則S∩（?_UT）=（　　）
A．{1，2} B．{1，2，3}
C．{1，2，4} D．{1，2，4，5，6，8}
組卷：98引用：2難度：0.7
解析
6．拋物線C：y²=-12x的焦點為F，P為拋物線C上一動點，定點A（-5，2），則|PA|+|PF|的最小值為（　　）
A．8 B．6 C．5 D．9
組卷：551引用：7難度：0.6
解析
7．已知雙曲線
C
：
x
2
a
2
-
y
2
b
2
=
1
（
a
＞
0
，
b
＞
0
）
的左焦點為F，O為坐標原點，P為雙曲線C的右支上一點，若
|
OP
|
=
3
a
，|PF|=3b,則雙曲線C的離心率為（　　）
A．
2
B．
3
C．
3
3
2
D．
5
2
組卷：94引用：3難度：0.6
解析
8．函數f（x）=（e^x+
1
e
x
）log₂|x|的圖象大致是（　　）
A． B． C． D．
組卷：218引用：1難度：0.7
解析
9．經過點A（3，2），且與直線4x+y-2=0平行的直線方程為（　　）
A．4x+y+2=0 B．4x+y-14=0 C．x-4y-12=0 D．x-4y-14=0
組卷：119引用：12難度：0.9
解析
10．系統找不到該試題

二.填空題（本大題共4個小題，每小題4分，共16分）

11．命題：
（1）一直線上有兩點到同一平面的距離相等說明直線與平面平行；
（2）與同一直線所成角相等的兩平面平行；
（3）與兩兩異面的三直線都相交的直線有無數條；
（4）四面體的四個面都可能是直角三角形；
以上命題正確的是：

．
組卷：13引用：2難度：0.5
解析
12．設
f
（
x
）
=
lg
1
-
ax
1
+
x
為奇函數；則a=
．
組卷：16引用：1難度：0.7
解析
13．設x,y滿足條件
y
≥
1
x
+
y
≤
2
x
-
2
y
+
4
≥
0
，則z=x+2y的最大值為
．
組卷：7引用：4難度：0.6
解析
14．已知正實數a,b,滿足ae²（lnb-lna+a-1）≥be^a，則
1
b
的最小值為
．
組卷：13引用：2難度：0.4
解析

三、解答題（本大題共5個小題，共48分.解答應寫出必要的文字說明、證明過程或演算步，驟.）

15．設橢圓
x
2
a
2
+
y
2
b
2
=
1
（
a
＞
b
＞
0
）
的左右頂點分別為A，B，點P在橢圓上且異于A，B兩點，O為坐標原點．
（1）若直線AP與BP的斜率之積為
-
1
2
，求橢圓的離心率；
（2）若|AP|=|OA|，證明直線OP的斜率k滿足|k|＞
3
．
組卷：1613引用：13難度：0.5
解析
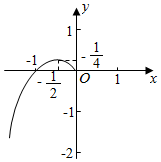16．定義在R上的偶函數f（x）在y軸左方（含原點）的圖象如圖所示，且解析式為f（x）=ax²+bx+c（a≠0，x≤0）．
（1）補全函數f（x）的圖象；
（2）求出函數f（x）的解析式；
（3）討論方程f（x）=d的根的個數；
（4）作出y=|f（x）|的圖象．
組卷：15引用：3難度：0.5
解析
17．函數y=f（x）的圖象為自原點出發的一條折線，當n-1≤y≤n（n∈N^*）時，該函數圖象是斜率為bⁿ（b≠0）的一條線段．已知數列{a_n}由
f
（
a
n
）
=
n
（
n
∈
N
*
）
定義．
（1）用b表示a₁，a₂；
（2）若b=2，記T_n=a₁+2a₂+?+na_n，求證：
T
n
＞
n
2
+
n
-
4
2
．
組卷：398引用：4難度：0.4
解析
18．已知函數f（x）=（lnx+ax+1）e^-x，其中常數a∈R．
（1）當a≥0時，討論f（x）的單調性；
（2）當
a
=
-
3
2
e
時，是否存在整數m使得關于x的不等式2m≥f（x）?x?e^x+3在區間（0，e）內有解？若存在，求出整數m的最小值；若不存在，請說明理由．
參考數據：ln2≈0.69，e≈2.72，e²≈7.39，e^-2≈0.14
組卷：123引用：2難度：0.1
解析
19．橢圓
x
2
a
2
+
y
2
b
2
=
1
（
a
＞
b
＞
0
）
的一個焦點是F（1，0），已知橢圓短軸的兩個三等分點與一個焦點構成正三角形．
（1）求橢圓的標準方程；
（2）已知Q（x₀，y₀）為橢圓上任意一點，求以Q為切點，橢圓的切線方程．
（3）設點P為直線x=4上一動點，過P作橢圓兩條切線PA，PB，求證直線AB過定點，并求出該定點的坐標．
組卷：80引用：1難度：0.1
解析

附加題：（本大題共2個小題，共16分）

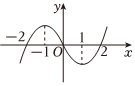20．已知定義在R上的可導三次函數f（x）的圖象如圖所示，f′（x）為函數f（x）的導函數，則不等式x?f′（x）＜0的解集為
．
組卷：6引用：0難度：0.7
解析
21．已知
f
（
x
）
=
3
si
n
4
x
+
（
sinx
+
cosx
）
2
-
3
co
s
4
x

（1）求f（x）的最小值及取最小值時x的集合；
（2）求f（x）在
x
∈
[
0
，
π
2
]
時的值域；
（3）求f（x）在
x
∈
[
-
π
2
，
π
2
]
時的單調遞減區間．
組卷：51引用：4難度：0.3
解析

0/60 進入組卷

0/20 進入試卷籃

布置作業 發布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

A．向左平移1個單位	B．向右平移1個單位
C．向左平移 1 3 個單位	D．向右平移 1 3 個單位

A．{1，2}	B．{1，2，3}
C．{1，2，4}	D．{1，2，4，5，6，8}

2021-2022學年陜西省西安市高新一中高二（上）期中數學試卷（理科）

一、選擇題（本大題共10個小題，每小題4分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的）

1．記等差數列{an}的前n項和為Sn．若a3+a13=a9，則下列一定成立的是（ ）

2．給出下列結論，其中不正確的是（ ）

3．為了得到函數y=cos（3x-1）的圖象，只需把y=cos3x的圖象上的所有點（ ）

4．已知向量a，b滿足|a|=1，|b|=2，且a與b的夾角為π3，則向量a-b與b的夾角為（ ）

5．設集合U={x∈N|0＜x≤8}，S={1，2，3，4，5}，T={3，5，7}，則S∩（?UT）=（ ）

6．拋物線C：y2=-12x的焦點為F，P為拋物線C上一動點，定點A（-5，2），則|PA|+|PF|的最小值為（ ）

7．已知雙曲線C：x2a2-y2b2=1（a＞0，b＞0）的左焦點為F，O為坐標原點，P為雙曲線C的右支上一點，若|OP|=3a，|PF|=3b,則雙曲線C的離心率為（ ）

8．函數f（x）=（ex+1ex）log2|x|的圖象大致是（ ）

9．經過點A（3，2），且與直線4x+y-2=0平行的直線方程為（ ）

二.填空題（本大題共4個小題，每小題4分，共16分）

12．設f（x）=lg1-ax1+x為奇函數；則a=．

13．設x,y滿足條件y≥1x+y≤2x-2y+4≥0，則z=x+2y的最大值為 ．

14．已知正實數a,b,滿足ae2（lnb-lna+a-1）≥bea，則1b的最小值為 ．

三、解答題（本大題共5個小題，共48分.解答應寫出必要的文字說明、證明過程或演算步，驟.）

15．設橢圓x2a2+y2b2=1（a＞b＞0）的左右頂點分別為A，B，點P在橢圓上且異于A，B兩點，O為坐標原點．（1）若直線AP與BP的斜率之積為-12，求橢圓的離心率；（2）若|AP|=|OA|，證明直線OP的斜率k滿足|k|＞3．

17．函數y=f（x）的圖象為自原點出發的一條折線，當n-1≤y≤n（n∈N*）時，該函數圖象是斜率為bn（b≠0）的一條線段．已知數列{an}由f（an）=n（n∈N*）定義．（1）用b表示a1，a2；（2）若b=2，記Tn=a1+2a2+?+nan，求證：Tn＞n2+n-42．

附加題：（本大題共2個小題，共16分）

20．已知定義在R上的可導三次函數f（x）的圖象如圖所示，f′（x）為函數f（x）的導函數，則不等式x?f′（x）＜0的解集為 ．

21．已知f（x）=3sin4x+（sinx+cosx）2-3cos4x（1）求f（x）的最小值及取最小值時x的集合；（2）求f（x）在x∈[0，π2]時的值域；（3）求f（x）在x∈[-π2，π2]時的單調遞減區間．

1．記等差數列{a_n}的前n項和為S_n．若a₃+a₁₃=a₉，則下列一定成立的是（　　）

2．給出下列結論，其中不正確的是（　　）

3．為了得到函數y=cos（3x-1）的圖象，只需把y=cos3x的圖象上的所有點（　　）

4．已知向量
a
，
b
滿足|
a
|=1，|
b
|=2，且
a
與
b
的夾角為
π
3
，則向量
a
-
b
與
b
的夾角為（　　）

5．設集合U={x∈N|0＜x≤8}，S={1，2，3，4，5}，T={3，5，7}，則S∩（?_UT）=（　　）

6．拋物線C：y²=-12x的焦點為F，P為拋物線C上一動點，定點A（-5，2），則|PA|+|PF|的最小值為（　　）

7．已知雙曲線
C
：
x
2
a
2
-
y
2
b
2
=
1
（
a
＞
0
，
b
＞
0
）
的左焦點為F，O為坐標原點，P為雙曲線C的右支上一點，若
|
OP
|
=
3
a
，|PF|=3b,則雙曲線C的離心率為（　　）

8．函數f（x）=（e^x+
1
e
x
）log₂|x|的圖象大致是（　　）

9．經過點A（3，2），且與直線4x+y-2=0平行的直線方程為（　　）

12．設
f
（
x
）
=
lg
1
-
ax
1
+
x
為奇函數；則a=
．

13．設x,y滿足條件
y
≥
1
x
+
y
≤
2
x
-
2
y
+
4
≥
0
，則z=x+2y的最大值為
．

14．已知正實數a,b,滿足ae²（lnb-lna+a-1）≥be^a，則
1
b
的最小值為
．

15．設橢圓
x
2
a
2
+
y
2
b
2
=
1
（
a
＞
b
＞
0
）
的左右頂點分別為A，B，點P在橢圓上且異于A，B兩點，O為坐標原點．
（1）若直線AP與BP的斜率之積為
-
1
2
，求橢圓的離心率；
（2）若|AP|=|OA|，證明直線OP的斜率k滿足|k|＞
3
．

20．已知定義在R上的可導三次函數f（x）的圖象如圖所示，f′（x）為函數f（x）的導函數，則不等式x?f′（x）＜0的解集為
．

21．已知
f
（
x
）
=
3
si
n
4
x
+
（
sinx
+
cosx
）
2
-
3
co
s
4
x

（1）求f（x）的最小值及取最小值時x的集合；
（2）求f（x）在
x
∈
[
0
，
π
2
]
時的值域；
（3）求f（x）在
x
∈
[
-
π
2
，
π
2
]
時的單調遞減區間．