2022-2023學年河南省許昌市禹州高級中學菁華校區高二（上）測評數學試卷（1月份）

一、單項選擇題：

• 1．已知集合A={x|-1＜x＜3}，B={-1，1，2}，則A∩B=（　　）

  A．{1，2}

  B．{-1，1，2}

  C．{0，1，2}

  D．{-1，0，1，2，3}
  組卷：74引用：11難度：0.9

  解析

• 2．已知復數z滿足（8+6i）z=5+12i,則|z|=（　　）

  A． 13 7 20

  B． 13 10

  C． 17 14

  D． 15 13
  組卷：4引用：3難度：0.8

  解析

• 3．甲和乙兩人各投籃一次，已知甲投中的概率是0.8，乙投中的概率是0.6，則恰有一人投中的概率為（　　）

  A．0.44

  B．0.48

  C．0.88

  D．0.98
  組卷：165引用：3難度：0.7

  解析

• 4．圓C₁：x²+y²-4x-16=0與圓C₂：x²+（y+1）²=5的位置關系是（　　）

  A．相交

  B．外切

  C．內切

  D．相離
  組卷：154引用：7難度：0.8

  解析

• 5．如圖，哈雷彗星圍繞太陽運動的軌跡是一個非常扁的橢圓，太陽位于橢圓軌跡的一個焦點上，已知哈雷彗星離太陽最近的距離為8.75×10¹⁰m,最遠的距離為5.30×10¹²m.若太陽的半徑忽略不計，則該橢圓軌跡的離心率約為（　　）

  A．0.88

  B．0.91

  C．0.97

  D．0.99
  組卷：71引用：4難度：0.7

  解析

• 6．已知雙曲線C的漸近線方程為2x±3y=0，且經過點

  （

  3

  2

  ，

  2

  ）

  ，則C的標準方程為（　　）

  A． x 2 9 - y 2 4 = 1

  B． x 2 12 - y 2 8 = 1

  C． y 2 4 - x 2 9 = 1

  D． y 2 2 - x 2 18 = 1
  組卷：210引用：4難度：0.7

  解析

• 7．已知點A（-1，0），B（1，0），動點P滿足

  PA

  2

  =

  3

  PB

  2

  ，則點P的軌跡方程為（　　）

  A． x 2 3 + y 2 2 = 1	B． x 2 4 + y 2 3 = 1
  C．x2+y2+4x-1=0	D．x2+y2-4x+1=0
  組卷：65引用：3難度：0.7

  解析

三、解答題：本大題共6小題，共70分.解答應寫出文字說明，證明過程或演算步驟.

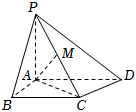• 21．如圖，四棱錐P-ABCD中，底面ABCD為直角梯形，

  ∠

  ABC

  =∠

  BAD

  =

  π

  2

  ，PA⊥平面ABCD，AD=2，BC=AB=1，M為PC的中點．
  （1）求證：平面PAC⊥平面PCD；
  （2）若AM⊥PC，求四棱錐P-ABCD的體積．
  （3）在（2）的條件下，求二面角P-CD-A的大小．
  組卷：76引用：2難度：0.6

  解析

• 22．在平面直角坐標系xOy中，直線AB與拋物線C：y²=2px（p＞0）交于點A、B．設直線OA、OB的斜率分別為k₁、k₂．
  （1）若直線AB經過拋物線C的焦點F，證明：k₁k₂=-4．
  （2）若k₁+k₂=λ（λ為常數），直線AB是否經過某個定點？若經過，求出這個定點；若不經過，請說明理由．
  組卷：104引用：2難度：0.5

  解析