2022-2023學年四川省綿陽市涪城區南山中學實驗學校英才班高三（上）月考數學試卷（理科）（12月份）

一、選擇題：本大題共12小題，每小題5分，共60分．在每小題給出的四個選項中，只有一項是符合題目要求的．

• 1．集合M={（x,y）|2x+y=0}，N={（x,y）|x+y-3=0}，則M∩N=（　　）

  A．{-3，6}

  B．（-3，6）

  C．{（-3，6）}

  D．{（3，-6）}
  組卷：58引用：6難度：0.8

  解析

• 2．已知直線2x+y-8=0與直線3x+（1-a）y+3=0平行，則a的值為（　　）

  A． - 1 2

  B． 1 2

  C．-5

  D．7
  組卷：75引用：4難度：0.8

  解析

• 3．已知a,b∈R，則下列命題正確的是（　　）

  A．若a＞b,則|a|＞|b|	B．若a≠b,則|a|≠|b|
  C．若a＞|b|，則a2＞b2	D．若a＜|b|，則a2＜b2
  組卷：59引用：4難度：0.7

  解析

• 4．圓C₁：（x-m）²+（y+2）²=9與圓C₂：（x+1）²+（y-m）²=4外切，則m的值為（　　）

  A．2

  B．-5

  C．2或-5

  D．不確定
  組卷：298引用：16難度：0.9

  解析

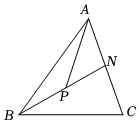• 5．如圖，在△ABC中，

  AN

  =

  1

  2

  AC

  ，P是BN的中點，若

  AP

  =

  m

  AB

  +

  n

  AC

  ，則m+n=（　　）

  A． 1 2

  B．1

  C． 3 2

  D． 3 4
  組卷：1517引用：11難度：0.8

  解析

• 6．若圓C：x²+y²-2（m-1）x+2（m-1）y+2m²-6m+4=0過坐標原點，則實數m的值為（　　）

  A．2或1

  B．-2或-1

  C．2

  D．1
  組卷：750引用：15難度：0.9

  解析

• 7．北宋科學家沈括在《夢溪筆談》中首創隙積術，是研究某種物品按一定規律堆積起來求其總數問題．南宋數學家楊輝在《詳解九章算法》和《算法通變本末》中，發展了隙積術的成果，對高階等差數列求和問題提出了一些新的垛積公式．高階等差數列的前后兩項之差并不相等，但是逐項差數之差或者高次成等差數列．現有二階等差數列：2，3，5，8，12，17，23…則該數列的第41項為（　　）

  A．782

  B．822

  C．780

  D．820
  組卷：35引用：4難度：0.7

  解析

選考題：共10分．請考生在第22、23題中任選一題做答．如果多做，則按所做的第一題記分．[選修4-4：坐標系與參數方程]?

• 22．在直角坐標系xoy中，直線l的參數方程為

  x = 2 2 t + 1

  y = 2 2 t

  （t為參數），曲線C的參數方程為

  x = 3 sinα + 3 cosα

  y = 3 sinα - 3 cosα

  （α為參數）．
  （1）求直線l與曲線C的普通方程，并說明C是什么曲線？
  （2）設M，N是直線l與曲線C的公共點，點P的坐標為（1，0），求|PM|-|PN|的值．
  組卷：151引用：4難度：0.5

  解析

[選修4-5：不等式選講]?

• 23．已知函數f（x）=|x+1|+2|x-1|．
  （1）求不等式f（x）＜8的解集；
  （2）設函數g（x）=f（x）-|x-1|的最小值為m,且正實數a,b,c滿足a+b+c=m,求證：

  a

  2

  b

  +

  b

  2

  c

  +

  c

  2

  a

  ≥2．
  組卷：36引用：9難度：0.6

  解析