2023-2024學(xué)年廣東省廣州市中山大學(xué)附中高三（上）期中數(shù)學(xué)試卷

一、選擇題：本大題共8小題，每小題5分，共40分，每小題只有一項(xiàng)是符合題目要求的．

• 1．已知a,b∈R，a-2i=（b-i）i,若z=a+bi,則

  z

  的虛部是（　　）

  A．2

  B．1

  C．-2i

  D．2i
  組卷：108引用：15難度：0.9

  解析

• 2．△ABC的內(nèi)角A，B，C的對(duì)邊分別為a、b、c,已知

  cos

  A

  =

  4

  5

  ，

  B

  =

  π

  3

  ，

  b

  =

  5

  3

  ，則a=（　　）

  A．6

  B． 6

  C．8

  D． 2 2
  組卷：266引用：4難度：0.5

  解析

• 3．公比不為1的等比數(shù)列{a_n}滿足a₅a₆+a₄a₇=18，若a₁a_m=9，則m的值為（　　）

  A．8

  B．9

  C．10

  D．11
  組卷：239引用：3難度：0.9

  解析

• 4．函數(shù)

  y

  =

  ln

  |

  x

  |

  x

  2

  +

  2

  的圖像大致為（　　）

  A．

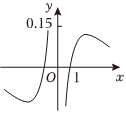
  B．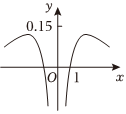

  C．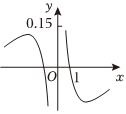

  D．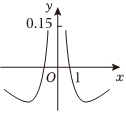
  組卷：172引用：12難度：0.7

  解析

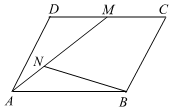• 5．如圖，在平行四邊形ABCD中，M是邊CD的中點(diǎn)，N是AM的一個(gè)三等分點(diǎn)（|AN|＜|NM|），若存在實(shí)數(shù)λ和μ，使得

  BN

  =

  λ

  AB

  +

  μ

  AD

  ，則λ+μ=（　　）

  A． 5 4

  B． 1 2

  C． - 1 2

  D． - 5 4
  組卷：568引用：6難度：0.9

  解析

• 6．已知函數(shù)f（x）滿足f（x+3）=-f（x），當(dāng)x∈[-3，0）時(shí)，f（x）=2^x+sin

  πx

  3

  ，則f（2023）=（　　）

  A． 1 4 - 3 2

  B．- 1 4

  C． 3 4

  D．- 1 4 + 3 2
  組卷：856引用：16難度：0.7

  解析

• 7．已知函數(shù)

  f

  （

  x

  ）

  =

  2

  sin

  （

  ωx

  +

  φ

  ）

  （

  ω

  ＞

  0

  ，-

  π

  2

  ＜

  φ

  ＜

  π

  2

  ）

  圖象的相鄰兩條對(duì)稱軸之間的距離為

  π

  6

  ，且關(guān)于點(diǎn)

  （

  5

  π

  18

  ，

  0

  ）

  對(duì)稱，則φ的值為（　　）

  A． π 12

  B． π 6

  C． π 4

  D． π 3
  組卷：205引用：4難度：0.5

  解析

四、解答題：本大題共6小題，共70分．解答應(yīng)寫出文字說(shuō)明、證明過(guò)程或演算步驟．

• 21．已知函數(shù)f（x）=x³-x,g（x）=2x-3．
  （Ⅰ）求曲線y=f（x）在點(diǎn)（1，f（1））處的切線方程；
  （Ⅱ）求函數(shù)f（x）在[0，2]上的最大值；
  （Ⅲ）求證：存在唯一的x₀，使得f（x₀）=g（x₀）．
  組卷：117引用：9難度：0.3

  解析

• 22．已知拋物線C₁：x²=4y的焦點(diǎn)F也是橢圓C₂：

  y

  2

  a

  2

  +

  x

  2

  b

  2

  =1（a＞b＞0）的一個(gè)焦點(diǎn)，C₁與C₂的公共弦長(zhǎng)為2

  6

  ．
  （1）求橢圓C₂的方程；
  （2）過(guò)點(diǎn)F作斜率為k的直線l與C₁交于A，B兩點(diǎn)，與C₂交于C，D兩點(diǎn)，且

  AC

  與

  BD

  同向．
  （i）當(dāng)直線l繞點(diǎn)F旋轉(zhuǎn)時(shí)，判斷△OAB的形狀；
  （ii）若|AC|=|BD|，求直線l的斜率．
  組卷：96引用：2難度：0.5

  解析