當前位置：試卷中心 > 試卷詳情

《第2章圓錐曲線與方程》2010年單元測試卷（2）

發布：2024/4/20 14:35:0

一、選擇題（共10小題，每小題3分，滿分30分）

1．已知雙曲線
x
2
a
2
-
y
2
b
2
=
1
的焦點到漸近線的距離為
2
3
，且雙曲線右支上一點P到右焦點的距離的最小值為2，則雙曲線的離心率為（　　）
A．
3
B．3 C．2 D．
1
2
組卷：41引用：5難度：0.7
解析
2．已知直線y=k（x+2）（k＞0）與拋物線C：y²=8x相交于A、B兩點，F為C的焦點，若|FA|=2|FB|，則k=（　　）
A．
1
3
B．
2
3
C．
2
3
D．
2
2
3
組卷：4674引用：93難度：0.7
解析
3．F₁，F₂分別是雙曲線
x
2
a
2
-
y
2
b
2
=1的左、右焦點，A是其右頂點，過F₂作x軸的垂線與雙曲線的一個交點為P，G是△PF₁F₂的重心，若
GA
?
F
1
F
2
=0，則雙曲線的離心率是（　　）
A．2 B．
2
C．3 D．
3
組卷：91引用：18難度：0.9
解析
4．雙曲線
x
2
b
2
-
y
2
a
2
=
1
的兩條漸近線互相垂直，那么該雙曲線的離心率是（　　）
A．2 B．
3
C．
2
D．
3
2
組卷：369引用：29難度：0.9
解析
5．F₁，F₂是橢圓
x
2
9
+
y
2
7
=
1
的兩個焦點，A為橢圓上一點，且向量
A
F
1
與
F
1
F
2
的夾角為
3
π
4
，則△AF₁F₂的面積為（　　）
A．7 B．
7
4
C．
7
2
D．
7
5
2
組卷：25引用：1難度：0.9
解析
6．以橢圓
x
2
16
+
y
2
9
=1的頂點為頂點，離心率為2的雙曲線方程是（　　）
A．
x
2
16
-
y
2
48
=
1
B．
y
2
9
-
x
2
27
=
1
C．
x
2
16
-
y
2
48
=
1
或
y
2
9
-
x
2
27
=
1
D．以上都不對
組卷：214引用：14難度：0.7
解析
7．若m是2和8的等比中項，則圓錐曲線x²+
y
2
m
=
1
的離心率為（　　）
A．
3
2
B．
5
C．
3
2
或
5
2
D．
3
2
或
5
組卷：1274引用：83難度：0.9
解析
8．設F₁和F₂為雙曲線
x
2
a
2
-
y
2
b
2
=1（a＞0，b＞0）的兩個焦點，若F₁，F₂，P（0，2b）是正三角形的三個頂點，則雙曲線的離心率為（　　）
A．
3
2
B．2 C．
5
2
D．3
組卷：493引用：40難度：0.9
解析
9．雙曲線
x
2
4
+
y
2
k
=
1
的離心率e∈（1，2），則k的取值范圍是（　　）
A．（-∞，0） B．（-3，0） C．（-12，0） D．（-60，-12）
組卷：96引用：20難度：0.9
解析
10．已知拋物線C：y²=2px（p＞0），過點A（
p
2
，0）的直線與拋物線C交于M，N兩點，且
MA
=
2
AN
，過點M，N向直線x=-
p
2
作垂線，垂足分別為P，Q，△MAP，△NAQ的面積分別為記為S₁與S₂，那么（　　）
A．S₁：S₂=2：1 B．S₁：S₂=5：2 C．S₁：S₂=4：1 D．S₁：S₂=7：1
組卷：57引用：4難度：0.5
解析

二、填空題（共9小題，每小題4分，滿分32分）

11．過橢圓
x
2
a
2
+
y
2
b
2
=
1
的左焦點F且傾斜角為60°的直線交橢圓于A、B兩點，若
|
AF
|
=
2
|
FB
|
，則橢圓的離心率e=
．
組卷：125引用：6難度：0.5
解析
12．拋物線y=ax²的準線方程是y=
1
2
，則a=
．
組卷：70引用：6難度：0.7
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

三、解答題（共18小題，滿分0分）

36．已知橢圓
x
2
a
2
+
y
2
b
2
=1（a＞b＞0）的離心率e=
6
3
，過點A（O，-b）和B（a,o）的直線到原點的距離為
3
2
．
（I）求橢圓的方程；
（Ⅱ）若直線y=kx+2（k≠o）與橢圓交于C、D兩點．問：是否存在常數k,使得以CD為直徑的圓過坐標原點？若存在，求出k,若不存在，請說明理由．
組卷：126引用：3難度：0.3
解析
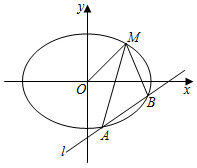37．如圖，已知橢圓的中心在原點，焦點在x軸上，長軸長是短軸長的2倍且經過點M（2，1），平行于OM的直線l在y軸上的截距為m（m≠0），l交橢圓于A、B兩個不同點．
（1）求橢圓的方程；
（2）求m的取值范圍；
（3）求證直線MA、MB與x軸始終圍成一個等腰三角形．
組卷：611引用：40難度：0.5
解析

0/60 進入組卷

0/20 進入試卷籃

布置作業 發布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

《第2章 圓錐曲線與方程》2010年單元測試卷（2）

一、選擇題（共10小題，每小題3分，滿分30分）

1．已知雙曲線x2a2-y2b2=1的焦點到漸近線的距離為23，且雙曲線右支上一點P到右焦點的距離的最小值為2，則雙曲線的離心率為（ ）

2．已知直線y=k（x+2）（k＞0）與拋物線C：y2=8x相交于A、B兩點，F為C的焦點，若|FA|=2|FB|，則k=（ ）

3．F1，F2分別是雙曲線x2a2-y2b2=1的左、右焦點，A是其右頂點，過F2作x軸的垂線與雙曲線的一個交點為P，G是△PF1F2的重心，若GA?F1F2=0，則雙曲線的離心率是（ ）

4．雙曲線x2b2-y2a2=1的兩條漸近線互相垂直，那么該雙曲線的離心率是（ ）

5．F1，F2是橢圓x29+y27=1的兩個焦點，A為橢圓上一點，且向量AF1與F1F2的夾角為3π4，則△AF1F2的面積為（ ）

6．以橢圓x216+y29=1的頂點為頂點，離心率為2的雙曲線方程是（ ）

7．若m是2和8的等比中項，則圓錐曲線x2+y2m=1的離心率為（ ）

8．設F1和F2為雙曲線x2a2-y2b2=1（a＞0，b＞0）的兩個焦點，若F1，F2，P（0，2b）是正三角形的三個頂點，則雙曲線的離心率為（ ）

9．雙曲線x24+y2k=1的離心率e∈（1，2），則k的取值范圍是（ ）

10．已知拋物線C：y2=2px（p＞0），過點A（p2，0）的直線與拋物線C交于M，N兩點，且MA=2AN，過點M，N向直線x=-p2作垂線，垂足分別為P，Q，△MAP，△NAQ的面積分別為記為S1與S2，那么（ ）

二、填空題（共9小題，每小題4分，滿分32分）

11．過橢圓x2a2+y2b2=1的左焦點F且傾斜角為60°的直線交橢圓于A、B兩點，若|AF|=2|FB|，則橢圓的離心率e=．

12．拋物線y=ax2的準線方程是y=12，則a=．

三、解答題（共18小題，滿分0分）

《第2章圓錐曲線與方程》2010年單元測試卷（2）

1．已知雙曲線
x
2
a
2
-
y
2
b
2
=
1
的焦點到漸近線的距離為
2
3
，且雙曲線右支上一點P到右焦點的距離的最小值為2，則雙曲線的離心率為（　　）

2．已知直線y=k（x+2）（k＞0）與拋物線C：y²=8x相交于A、B兩點，F為C的焦點，若|FA|=2|FB|，則k=（　　）

3．F₁，F₂分別是雙曲線
x
2
a
2
-
y
2
b
2
=1的左、右焦點，A是其右頂點，過F₂作x軸的垂線與雙曲線的一個交點為P，G是△PF₁F₂的重心，若
GA
?
F
1
F
2
=0，則雙曲線的離心率是（　　）

4．雙曲線
x
2
b
2
-
y
2
a
2
=
1
的兩條漸近線互相垂直，那么該雙曲線的離心率是（　　）

5．F₁，F₂是橢圓
x
2
9
+
y
2
7
=
1
的兩個焦點，A為橢圓上一點，且向量
A
F
1
與
F
1
F
2
的夾角為
3
π
4
，則△AF₁F₂的面積為（　　）

6．以橢圓
x
2
16
+
y
2
9
=1的頂點為頂點，離心率為2的雙曲線方程是（　　）

7．若m是2和8的等比中項，則圓錐曲線x²+
y
2
m
=
1
的離心率為（　　）

8．設F₁和F₂為雙曲線
x
2
a
2
-
y
2
b
2
=1（a＞0，b＞0）的兩個焦點，若F₁，F₂，P（0，2b）是正三角形的三個頂點，則雙曲線的離心率為（　　）

9．雙曲線
x
2
4
+
y
2
k
=
1
的離心率e∈（1，2），則k的取值范圍是（　　）

10．已知拋物線C：y²=2px（p＞0），過點A（
p
2
，0）的直線與拋物線C交于M，N兩點，且
MA
=
2
AN
，過點M，N向直線x=-
p
2
作垂線，垂足分別為P，Q，△MAP，△NAQ的面積分別為記為S₁與S₂，那么（　　）

11．過橢圓
x
2
a
2
+
y
2
b
2
=
1
的左焦點F且傾斜角為60°的直線交橢圓于A、B兩點，若
|
AF
|
=
2
|
FB
|
，則橢圓的離心率e=
．

12．拋物線y=ax²的準線方程是y=
1
2
，則a=
．