2022-2023學年四川省成都市錦江區嘉祥外國語高級中學高一(下)月考數學試卷(6月份)
發布:2024/8/11 1:0:1
一、選擇題(本題共8小題,每小題5分,共40分.每小題給出的四個選項中,只有一項是符合題目要求的)
-
1.復數z=ai+b(a,b∈R)是純虛數的充分不必要條件是( )
A.a≠0且b=0 B.b=0 C.a=1且b=0 D.a=b=0 組卷:173引用:6難度:0.7 -
2.已知第二象限角α的終邊與單位圓交于
,則sin2α=( )P(m,35)A. -1225B. -2425C. 1225D. 2425組卷:106引用:5難度:0.7 -
3.已知菱形ABCD邊長為1,∠BAD=60°,則
=( )BD?DCA. 32B. -32C. 12D. -12組卷:184引用:2難度:0.8 -
4.已知直線l及三個互不重合的平面α,β,γ,下列結論錯誤的是( )
A.若α∥β,β∥γ,則α∥γ B.若α⊥β,β⊥γ,則α⊥γ C.若α⊥γ,α∥β,則β⊥γ D.若α⊥γ,β⊥γ,α∩β=l,則l⊥γ 組卷:101引用:4難度:0.7 -
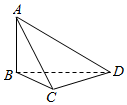 5.在我國古代數學名著《九章算術》中,將四個面都為直角三角形的四面體稱為鱉臑,如圖,在鱉臑ABCD中,AB⊥平面BCD,且AB=BC=CD,則異面直線AC與BD所成角的余弦值為( )
5.在我國古代數學名著《九章算術》中,將四個面都為直角三角形的四面體稱為鱉臑,如圖,在鱉臑ABCD中,AB⊥平面BCD,且AB=BC=CD,則異面直線AC與BD所成角的余弦值為( )A. 12B.- 12C. 32D.- 32組卷:557引用:20難度:0.7 -
6.歐拉公式eix=cosx+isinx(其中e是自然對數的底,i為虛數單位)是由著名數學家歐拉發現的,它將指數函數的定義域擴大到復數,建立了指數函數與三角函數的關系,被譽為“數學中的天橋”.根據歐拉公式,若將
所表示的復數記為z,則e2π3i=( )zA. 12+32iB. 12-32iC. -12+32iD. -12-32i組卷:25引用:3難度:0.8 -
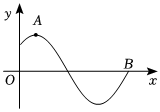 7.已知函數的部分圖象如下所示,其中f(x)=2cos(ωx+φ)(ω>0,|φ|<π2),為了得到g(x)=2sin2x的圖象,需將( )A(π12,2),B(7π12,0)
7.已知函數的部分圖象如下所示,其中f(x)=2cos(ωx+φ)(ω>0,|φ|<π2),為了得到g(x)=2sin2x的圖象,需將( )A(π12,2),B(7π12,0)A.函數f(x)的圖象的橫坐標伸長為原來的 倍后,再向左平移32個單位長度3π8B.函數f(x)的圖象的橫坐標縮短為原來的 后,再向右平移23個單位長度π8C.函數f(x)的圖象向左平移 個單位長度后,再將橫坐標伸長為原來的π4倍32D.函數f(x)的圖象向右平移 個單位長度后,再將橫坐標伸長為原來的π12倍32組卷:261引用:5難度:0.8
四、解答題(本題共6小題,共70分.解答應寫出文字說明,證明過程或演算步驟)
-
21.在直角梯形ABCD中,AD∥BC,
,∠ABC=90°(如圖1).把△ABD沿BD翻折,使得二面角A-BD-C的平面角為θ(如圖2),M、N分別是BD和BC中點.BC=2AD=2AB=22
(1)若E是線段BN的中點,動點F在三棱錐A-BMN表面上運動,并且總保持FE⊥BD,求動點F的軌跡的長度(可用θ表示),詳細說明理由;
(2)若P、Q分別為線段AB與DN上一點,使得,令PQ與BD和AN所成的角分別為θ1和θ2,求sinθ1+sinθ2的取值范圍.APPB=NQQD=λ(λ∈R)組卷:99引用:4難度:0.4 -
 22.如圖,已知三棱柱ABC-A1B1C1,平面A1ACC1⊥平面ABC,∠ABC=90°,
22.如圖,已知三棱柱ABC-A1B1C1,平面A1ACC1⊥平面ABC,∠ABC=90°,
∠BAC=30°,A1A=A1C=AC,E,F分別是AC,A1B1的中點.
(Ⅰ)證明:EF⊥BC;
(Ⅱ)求直線EF與平面A1BC所成角的余弦值.
(Ⅲ)求二面角A-A1C-B的正弦值.組卷:1321引用:7難度:0.5


