2018-2019學年安徽省六安一中高三（上）開學數學試卷（理科）

一、選擇題：本大題共12小題，每小題5分，共60分、每小題給出的四個選項中只有一項是符合題目要求的

• 1．已知復數z=

  （

  1

  -

  2

  i

  ）

  2

  2

  +

  i

  ，則復數z的模為（　　）

  A．5

  B． 5

  C． 3 10

  D． 5 2
  組卷：79引用：4難度：0.9

  解析

• 2．已知

  z

  是z的共軛復數，且

  |

  z

  |

  -

  z

  =

  1

  -

  2

  i

  ，則z的虛部是（　　）

  A．1

  B．-1

  C．2

  D．-2
  組卷：12引用：2難度：0.9

  解析

• 3．我國數學家陳景潤在哥德巴赫猜想的研究中取得了世界領先的成果．哥德巴赫猜想是“每個大于2的偶數可以表示為兩個素數的和”，如30=7+23．在不超過30的素數中，隨機選取兩個不同的數，其和等于30的概率是（　　）

  A． 1 12

  B． 1 14

  C． 1 15

  D． 1 18
  組卷：4546引用：27難度：0.7

  解析

• 4．已知|z₁|=|z₂|=|z₁-z₂|=1，則|z₁+z₂|等于（　　）

  A．1

  B． 2

  C． 3

  D．2 3
  組卷：24引用：5難度：0.9

  解析

• 5．若a₀x²⁰¹⁶+a₁x²⁰¹⁵（1-x）+a₂x²⁰¹⁴（1-x）²++a₂₀₁₆（1-x）²⁰¹⁶=1，則a₀+a₁+a₂++a₂₀₁₆的值為（　　）

  A．1

  B．0

  C．22016

  D．22015
  組卷：16引用：1難度：0.6

  解析

• 6．對33000分解質因數得33000=2³×3×5³×11，則33000的正偶數因數的個數是（　　）

  A．48

  B．72

  C．64

  D．96
  組卷：134引用：3難度：0.7

  解析

• 7．若n=2

  ∫

  3

  0

  xdx+1，則二項式（x²

  -

  1

  2

  x

  ）ⁿ的展開式中的常數項為（　　）

  A． 45 256

  B． - 45 256

  C． 45 128

  D． - 45 128
  組卷：164引用：2難度：0.7

  解析

三、解答題：本大題共6小題，共70分解答應寫出文字說明，證明過程或演算步驟

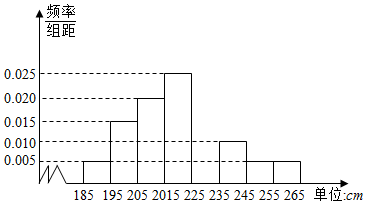• 21．2015年3月24日，習近平總書記主持召開中央政治局會議，通過了《關于加快推進生態文明建設的意見》，正式把“堅持綠水青山就是金山銀山”的理念寫進中央文件，成為指導中國加快推進生態文明建設的重要指導思想．為響應國家號召，某市2016年清明節期間種植了一批樹苗，兩年后市園林部門從這批樹苗中隨機抽取100棵進行跟蹤檢測，得到樹高的頻率分布直方圖如圖所示：
  （1）求樹高在225-235cm之間樹苗的棵數，并求這100棵樹苗樹高的平均值和方差（方差四舍五入保留整數）；
  （2）若將樹高以等級呈現，規定：樹高在185-205cm為合格，在205-235為良好，在235-265cm為優秀．視該樣本的頻率分布為總體的頻率分布，若從這批樹苗中隨機抽取3棵，求樹高等級為優秀的棵數ξ的分布列和數學期望；
  （3）經驗表明樹苗樹高X-N（μ，σ²），用樣本的平均值作為μ的估計值，用樣本的方差作為σ²的估計值，試求該批樹苗小于等于255.4cm的概率．
  （提供數據：

  271

  ≈

  16

  .

  45

  ，

  305

  ≈17.45，

  340

  ≈18.45）
  附：若隨機變量Z服從正態分布N（μ，σ²），則P（μ-σ＜Z≤μ+σ）=0.6826，P（μ-2σ＜Z≤μ+2σ）=0.9544，P（μ-3σ＜Z≤μ+3σ）=0.9974．
  組卷：157引用：3難度：0.5

  解析

• 22．已知函數f（x）=e^ax-ax-3（a≠0）
  （Ⅰ）求f（x）的極值；
  （Ⅱ）當a＞0時，設

  g

  （

  x

  ）

  =

  1

  a

  e

  ax

  -

  1

  2

  a

  x

  2

  -

  3

  x

  ，求證：曲線y=g（x）存在兩條斜率為-1且不重合的切線．
  組卷：362引用：6難度：0.1

  解析