2020-2021學年重慶八中高三（上）階段性數學試卷（3）

一、單選題：本題共8小題，每小題5分，共40分．在每小題給出的選項中，只有一項符合題目要求．

• 1．已知a,b均為實數，則|a|＜b是a+b＞0的（　　）

  A．充要條件	B．充分不必要條件
  C．必要不充分條件	D．既不充分也不必要條件
  組卷：7引用：1難度：0.7

  解析

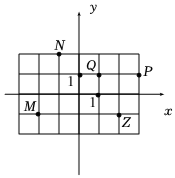• 2．設i為虛數單位，如圖，網格紙上小正方形的邊長為1，圖中復平面內點Z表示復數z,則表示復數（1+i）?z的點是（　　）

  A．M

  B．N

  C．P

  D．Q
  組卷：58引用：3難度：0.8

  解析

• 3．如果數列{a_n}是一個以q為公比的等比數列，b_n=-2a_n（n∈N^*），那么數列{b_n}是（　　）

  A．以q為公比的等比數列

  B．以-q為公比的等比數列

  C．以2q為公比的等比數列

  D．以-2q為公比的等比數列
  組卷：521引用：3難度：0.7

  解析

• 4．某人5次上班途中所花的時間（單位：分鐘）分別為x,y,10，11，9．已知這組數據的平均數為10，方差為2，則|x-y|的值為（　　）

  A．1

  B．2

  C．3

  D．4
  組卷：998引用：58難度：0.9

  解析

• 5．在△ABC中，B=

  π

  4

  ，BC邊上的高等于

  1

  3

  BC，則sinA=（　　）

  A． 3 10

  B． 10 10

  C． 5 5

  D． 3 10 10
  組卷：5805引用：35難度：0.7

  解析

• 6．現有某種細胞1千個，其中約有占總數一半的細胞每小時分裂一次，即由1個細胞分裂成2個細胞，按這種規律，1小時后，細胞總數約為

  1

  2

  ×

  1000

  +

  1

  2

  ×

  1000

  ×

  2

  =

  3

  2

  ×1000，2小時后，細胞總數約為

  1

  2

  ×

  3

  2

  ×

  1000

  +

  1

  2

  ×

  3

  2

  ×

  1000

  ×

  2

  =

  9

  4

  ×1000，問當細胞總數超過10¹⁰個時，所需時間約為（　　）（參考數據：lg3≈0.477，lg2≈0.301）

  A．34小時

  B．37小時

  C．40小時

  D．43小時
  組卷：49引用：4難度：0.7

  解析

• 7．已知x,y∈（0，+∞），2^x-4=（

  1

  4

  ）^y，則xy的最大值為（　　）

  A．2

  B． 9 8

  C． 3 2

  D． 9 4
  組卷：206引用：5難度：0.8

  解析

四、解答題：本題共6小題，滿分70分.

• 21．已知橢圓

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =1（a＞b＞0）的兩個焦點為F₁，F₂，離心率為

  3

  2

  ，P點是橢圓上某一點，△PF₁F₂的周長為4+2

  3

  ，
  （1）求橢圓的標準方程；
  （2）以橢圓的上頂點B為直角頂點作橢圓的內接等腰直角三角形ABC，設直線AB的斜率為k（k＞0），求所有滿足要求的k.
  組卷：55引用：2難度：0.8

  解析

• 22．函數

  f

  （

  x

  ）

  =

  1

  m

  e

  mx

  -

  1

  2

  x

  2

  ，f′（x）是f（x）的導函數．
  （1）若m=1，x∈R，證明：f（x）+f（-x）≥2；
  （2）若m＞1，且對任意x∈（e,+∞），

  mx

  （

  mx

  -

  6

  ）

  +

  2

  f

  ′

  （

  x

  ）

  lnx

  ≥

  lnx

  -

  6

  恒成立，求實數m的取值范圍．
  組卷：107引用：4難度：0.2

  解析