2022年天津市濱海新區塘沽一中高考數學三模試卷

一．選擇題：在每小題給出的四個選項中，只有一項是符合題目要求的

• 1．設集合A={1，2，6}，B={2，4}，C={x∈R|-1≤x≤5}，則（A∪B）∩C=（　　）

  A．{2}

  B．{1，2，4}

  C．{1，2，4，5}

  D．{x∈R|-1≤x≤5}
  組卷：5282引用：22難度：0.9

  解析

• 2．“lga＞lgb”是“（a-2）³＞（b-2）³”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充要條件	D．既不充分又不必要條件
  組卷：257引用：6難度：0.8

  解析

• 3．函數f（x）=

  x

  2

  -

  1

  e

  |

  x

  |

  的圖象大致為（　　）

  A．	B．
  C．	D．
  組卷：359引用：7難度：0.8

  解析

• 4．已知a=2^0.1，b=log₄3，c=log₅2，則（　　）

  A．a＞c＞b

  B．b＞c＞a

  C．a＞b＞c

  D．b＞a＞c
  組卷：602引用：6難度：0.9

  解析

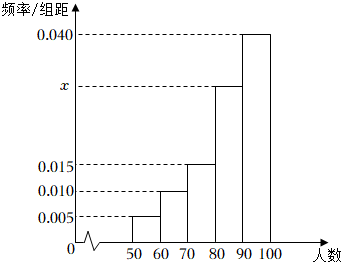• 5．某校隨機抽取了400名學生進行成績統計，發現抽取的學生的成績都在50分至100分之間，進行適當分組畫出頻率分布直方圖如圖所示，下列說法正確的是（　　）

  A．直方圖中x的值為0.040

  B．在被抽取的學生中，成績在區間[70，80）的學生數為30人

  C．估計全校學生的平均成績為84分

  D．估計全校學生成績的樣本數據的80%分位數約為93分
  組卷：1058引用：6難度：0.8

  解析

• 6．如圖所示的糧倉可近似為一個圓錐和圓臺的組合體，且圓錐的底面圓與圓臺的較大底面圓重合．已知圓臺的較小底面圓的半徑為1，圓錐與圓臺的高分別為

  5

  -1和3，則此組合體的外接球的表面積是（　　）

  A．16π

  B．20π

  C．24π

  D．28π
  組卷：429引用：8難度：0.7

  解析

三．解答題：本大題共5小題，共75分.解答應寫出文字說明，證明過程或演算步驟.

• 19．已知數列{a_n}，{b_n}，已知對于任意n∈N^*，都有

  a

  n

  =

  3

  b

  n

  +

  1

  ，數列{b_n}是等差數列，b₁=1，且b₂+5，b₄+1，b₆-3成等比數列．
  （1）求數列{a_n}和{b_n}的通項公式；
  （2）記

  c

  n

  =

  a n ， n = 2 k - 1

  b n 2 ， n = 2 k

  （

  k

  ∈

  N

  *

  ）

  ．
  （ⅰ）求

  n

  ∑

  i

  =

  1

  2

  log

  3

  c

  2

  i

  -

  1

  ?

  log

  3

  c

  2

  i

  +

  1

  ；
  （ⅱ）求

  2

  n

  ∑

  k

  =

  1

  c

  k

  c

  k

  +

  1

  ．
  組卷：429引用：3難度：0.5

  解析

• 20．已知函數

  f

  （

  x

  ）

  =

  （

  x

  +

  a

  ）

  lnx

  +

  a

  +

  1

  x

  ．
  （1）若函數f（x）在點（e,f（e））處的切線斜率為0，求a的值；
  （2）當a=1時．
  （ⅰ）設函數

  G

  （

  x

  ）

  =

  xf

  ′

  （

  x

  ）

  f

  （

  x

  ）

  ，求證：y=f（x）與y=G（x）在[1，e]上均單調遞增；
  （ⅱ）設區間I∈[x₀，x₀+1]（其中I?[1，e]，證明：存在實數λ＞1，使得函數F（x）=x²（f（x）-λf（x₀））在區間I上總存在極值點．
  組卷：178引用：1難度：0.4

  解析