2021-2022學年山東省青島實驗中學七年級(下)期中數學試卷
發布:2024/4/20 14:35:0
一、選擇題:(每道小題3分,共24分)
-
1.下列運算正確的是( )
A.-a2?a3=a5 B.a2?a3=a6 C.a2+a3=a5 D.(a2)3=a6 組卷:585引用:8難度:0.7 -
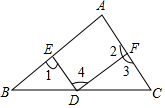
 2.如圖,下列說法不正確的是( )
2.如圖,下列說法不正確的是( )A.∠1與∠3是同位角 B.∠1與∠2是內錯角 C.∠C與∠2是同旁內角 D.∠A與∠2是同位角 組卷:473引用:7難度:0.7 -
3.在實驗課上,小亮利用同一塊木板測得小車從不同高度下滑的時間,支撐物高度(h)與下滑的時間(t)的關系如下表:
以下結論錯誤的是( )支撐物高h(cm) 10 20 30 40 50 … 下滑時間t(s) 3.25 3.01 2.81 2.66 2.56 … A.當h=40時,t約2.66秒 B.隨支撐物高度增加,下滑時間越來越短 C.支撐物高度每增加了10cm,時間就會減少0.24秒 D.估計當h=80cm時,t一定小于2.56秒 組卷:424引用:12難度:0.6 -
4.研究表明,某新型冠狀病毒體大小約為125納米也就是0.125微米,而95口罩能過濾0.3微米的顆粒,并不能將病毒過濾,口罩的作用是阻擋病毒傳播的“載體”,而非直接擋住病毒.1納米就是0.000000001米.那么0.3微米用科學記數法表示為( )
A.3×10-9米 B.0.3×10-8米 C.3×10-5米 D.3×10-7米 組卷:315引用:7難度:0.9 -
5.小明有足夠多的如圖所示的正方形卡片A,B和長方形卡片C,如果他要拼一個長為(a+2b),寬為(a+b)的大長方形,共需要C類卡片( )
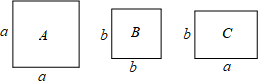
A.3張 B.4張 C.5張 D.6張 組卷:1498引用:8難度:0.8 -
 6.如圖,在下列給出的條件中,能判定AB∥DF的是( )
6.如圖,在下列給出的條件中,能判定AB∥DF的是( )A.∠1=∠A B.∠A=∠3 C.∠3=∠4 D.∠2+∠4=180° 組卷:271引用:3難度:0.7 -
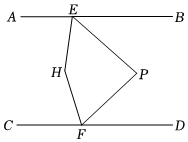 7.如圖,直線AB∥CD,點E,F分別在直線.AB和直線CD上,點P在兩條平行線之間,∠AEP和∠CFP的角平分線交于點H,已知∠P=88°,則∠H的度數為( )
7.如圖,直線AB∥CD,點E,F分別在直線.AB和直線CD上,點P在兩條平行線之間,∠AEP和∠CFP的角平分線交于點H,已知∠P=88°,則∠H的度數為( )A.92° B.156° C.136° D.141° 組卷:612引用:6難度:0.7 -
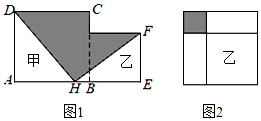 8.現有甲、乙兩個正方形紙片,將甲、乙并列放置后得到圖1,已知點H為AE的中點,連結DH,FH.將乙紙片放到甲的內部得到圖2.已知甲、乙兩個正方形邊長之和為8,圖2的陰影部分面積為6,則圖1的陰影部分面積為( )
8.現有甲、乙兩個正方形紙片,將甲、乙并列放置后得到圖1,已知點H為AE的中點,連結DH,FH.將乙紙片放到甲的內部得到圖2.已知甲、乙兩個正方形邊長之和為8,圖2的陰影部分面積為6,則圖1的陰影部分面積為( )A.19 B.28 C.77 D.21 組卷:1153引用:5難度:0.5
三、解答題(本題共72分)
-
24.現有長與寬分別為a、b的小長方形若干個,用兩個這樣的小長方形拼成如圖1的圖形,用四個相同的小長方形拼成圖2的圖形,請認真觀察圖形,解答下列問題:
(1)根據圖中條件,請寫出圖1和圖2所驗證的關于a、b的關系式:(用含a、b的代數式表示出來);
圖1表示:;
圖2表示:;
根據上面的解題思路與方法,解決下列問題:
(2)若x+y=8,x2+y2=40,求xy的值;
(3)請直接寫出下列問題答案:
①若2m+3n=5,mn=1,則2m-3n= ;
②若(4-m)(5-m)=6,則(4-m)2+(5-m)2= .
(4)如圖3,點C是線段AB上的一點,以AC,BC為邊向兩邊作正方形,設AB=7,兩正方形的面積和S1+S2=16,求圖中陰影部分面積.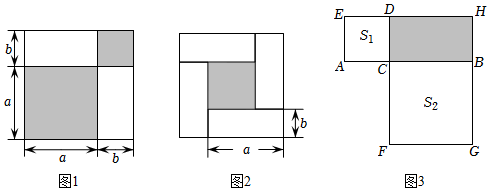 組卷:2179引用:10難度:0.6
組卷:2179引用:10難度:0.6 -
25.【閱讀理解】:兩條平行線間的拐點問題經常可以通過作一條直線的平行線進行轉化.例如:如圖1,MN∥PQ,點C、B分別在直線MN、PQ上,點A在直線MN、PQ之間.
求證:∠CAB=∠MCA+∠PBA;
證明:如圖1,過點A作AD∥MN,
∵MN∥PQ,AD∥MN,
∴AD∥MN∥PQ,
∴∠MCA=∠DAC,∠PBA=∠DAB,
∴∠CAB=∠DAC+∠DAB=∠MCA+∠PBA,
即:∠CAB=∠MCA+∠PBA;
【類比應用】已知直線AB∥CD,P為平面內一點,連接PA、PD.
(1)如圖2,已知∠A=50°,∠D=150°,求∠APD的度數,說明理由;
(2)如圖3,設∠PAB=α、∠CDP=β、直接寫出α、β、∠P之間的數量關系為 .
【聯系拓展】如圖4,直線AB∥CD,P為平面內一點,連接PA、PD.AP⊥PD,DN平分∠PDC,若∠PAN+∠PAB=∠P,運用(2)中的結論,求∠N的度數,說明理由.12 組卷:1111引用:8難度:0.4
組卷:1111引用:8難度:0.4


