當前位置：試卷中心 > 試卷詳情

2018-2019學年四川省成都外國語學校八年級（下）開學數(shù)學試卷

發(fā)布：2024/4/20 14:35:0

一、選擇題（每題3分，共30分，請將正確選項填涂在答題卡上）

1．函數(shù)y=
x
+
1
x
-
1
中自變量x的取值范圍是（　　）
A．x≥-1且x≠1 B．x≥-1 C．x≠1 D．-1≤x＜1
組卷：1418引用：14難度：0.9
解析
2．a,b都是實數(shù)，且a＜b,則下列不等式的變形正確的是（　　）
A．a(chǎn)+x＞b+x B．-a+1＜-b+1 C．3a＜3b D．
a
2
＞
b
2
組卷：2342引用：76難度：0.9
解析
3．P₁（x₁，y₁），P₂（x₂，y₂）是正比例函數(shù)y=-2x圖象上的兩點，則下列判斷正確的是（　　）
A．y₁＞y₂ B．y₁＜y₂
C．當x₁＜x₂時，y₁＞y₂ D．當x₁＜x₂時，y₁＜y₂
組卷：500引用：5難度：0.7
解析
4．如果A（1-a,b+1）在第三象限，那么點B（a,b）在（　　）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
組卷：1196引用：8難度：0.7
解析
5．已知
x
=
2
y
=
1
是二元一次方程組
mx
+
ny
=
8
nx
-
my
=
1
的解，則
m
+
3
n
的算術平方根為（　　）
A．±3 B．3 C．
3
D．
±
3
組卷：4689引用：6難度：0.7
解析
6．由下列條件不能判定△ABC為直角三角形的是（　　）
A．∠A+∠C=∠B B．a(chǎn)=
1
3
，b=
1
4
，c=
1
5
C．（b+a）（b-a）=c² D．∠A：∠B：∠C=5：3：2
組卷：1336引用：36難度：0.7
解析

7．下表記錄了甲、乙、丙、丁四名跳遠運動員選拔賽成績的平均數(shù)
x
與方差s²：

甲乙丙丁

平均數(shù)
x
（cm） 561 560 561 560

方差s²（cm²） 3.5 3.5 15.5 16.5

根據(jù)表中數(shù)據(jù)，要從中選擇一名成績好又發(fā)揮穩(wěn)定的運動員參加比賽，應該選擇（　　）

A．甲

B．乙

C．丙

D．丁

組卷：2414引用：89難度：0.9

解析

8．已知，如圖長方形ABCD中，AB=3cm,AD=9cm,將此長方形折疊，使點B與點D重合，折痕為EF，則△ABE的面積為（　　）
A．3cm² B．4cm² C．6cm² D．12cm²
組卷：10343引用：134難度：0.5
解析
9．將直線y=2x-3向右平移2個單位，再向上平移3個單位后，所得的直線的表達式為（　　）
A．y=2x-4 B．y=2x+4 C．y=2x+2 D．y=2x-2
組卷：7774引用：40難度：0.9
解析

當前模式為游客模式，立即登錄查看試卷全部內(nèi)容及下載

二、解答題（共30分）

27．閱讀下列材料：
小明遇到一個問題：在△ABC中，AB，BC，AC三邊的長分別為
5
、
10
、
13
，求△ABC的面積．小明是這樣解決問題的：如圖1所示，先畫一個正方形網(wǎng)格（每個小正方形的邊長為1），再在網(wǎng)格中畫出格點△ABC（即△ABC三個頂點都在小正方形的頂點處），從而借助網(wǎng)格就能計算出△ABC的面積．他把這種解決問題的方法稱為構圖法．
參考小明解決問題的方法，完成下列問題：
（1）圖2是一個6×6的正方形網(wǎng)格（每個小正方形的邊長為1）．
①利用構圖法在答卷的圖2中畫出三邊長分別為
13
、
20
、
29
的格點△DEF；
②計算①中△DEF的面積為
；（直接寫出答案）
（2）如圖3，已知△PQR，以PQ，PR為邊向外作正方形PQAF，正方形PRDE，連接EF．
①判斷△PQR與△PEF面積之間的關系，并說明理由．
②若PQ=
10
，PR=
13
，QR=3，直接寫出六邊形AQRDEF的面積為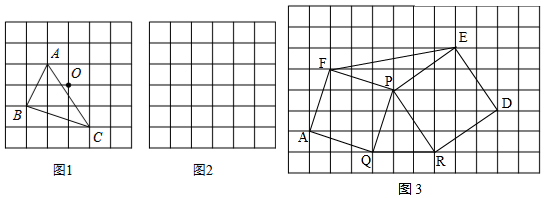
．
組卷：1792引用：6難度：0.3
解析
28．如圖1，平面直角坐標系中，直線y=kx+b與x軸交于點A（6，0），與y軸交于點B，與直線y=2x交于點C（a,4）．
（1）求點C的坐標及直線AB的表達式；
（2）如圖2，在（1）的條件下，過點E作直線l⊥x軸于點E，交直線y=2x于點F，交直線y=kx+b于點G，若點E的坐標是（4，0）．
①求△CGF的面積；
②直線l上是否存在點P，使OP+BP的值最小？若存在，直接寫出點P的坐標；若不存在，說明理由；
（3）若（2）中的點E是x軸上的一個動點，點E的橫坐標為m（m＞0），當點E在x軸上運動時，探究下列問題：
請從A，B兩題中任選一題作答，我選擇
題：
A．當m取何值時，直線l上存在點Q，使得以A，C，Q為頂點的三角形與△AOC全等？請直接寫出相應的m的值．
B．當△BFG是等腰三角形時直接寫出m的值．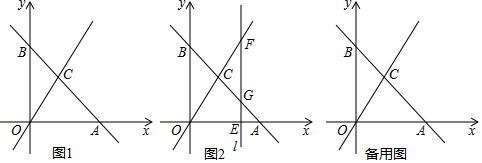
組卷：2186引用：3難度：0.2
解析