當前位置：試卷中心 > 試卷詳情

2023-2024學年山東省青島一中市南分校八年級（上）期中數學試卷

發布：2024/10/5 9:0:2

一、選擇題（本大題共8小題，每小題3分，共24分）在每個題給出的四個選項中，只有一項是符合題目要求的.

1．下列各數是無理數的是（　　）
A．-5 B．
3
C．6.8 D．
11
7
組卷：28引用：1難度：0.8
解析
2．若電影票上小明的座號“5排6座”記作（5，6），則小強的座號“6排7座”可記作（　　）
A．（-6，7） B．（6，7） C．（7，6） D．（-6，-7）
組卷：106引用：1難度：0.5
解析
3．下列四組數據中，能作為直角三角形三邊長的是（　　）
A．
6
，
8
，
10
B．3²，4²，5² C．9，40，41 D．
6
5
，
12
5
，
13
5
組卷：417引用：5難度：0.5
解析
4．如圖，矩形寬為1，已知OA=OB，點A表示的數為a,則下列說法正確的是（　　）
A．a的值為
10
B．a的值為-3.1
C．a的相反數為
10
D．a的倒數為
10
10
組卷：296引用：2難度：0.6
解析
5．正比例函數y=kx,當x=2時，y=-1，則此正比例函數的關系式為（　　）
A．y=2x B．y=
1
2
x C．y=-
1
2
x D．y=-2x
組卷：371引用：4難度：0.7
解析
6．2、5、m是某三角形三邊的長，則
（
m
-
3
）
2
+
（
m
-
7
）
2
等于（　　）
A．2m-10 B．10-2m C．10 D．4
組卷：3948引用：38難度：0.7
解析
7．如圖是做課間操時小明、小剛和小紅三人的相對位置，如果用（2，3）表示小明的位置，（0，2）表示小剛的位置，則小紅的位置可表示為（　　）
A．（-1，-1） B．（0，0） C．（1，0） D．（1，1）
組卷：177引用：6難度：0.9
解析
8．一次函數y=kx+b與正比例函數y=kbx,k,b是常數，且kb≠0的圖象可能是（　　）
A． B． C． D．
組卷：2300引用：10難度：0.6
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

三、解答題（本大題共8小題，共72分）

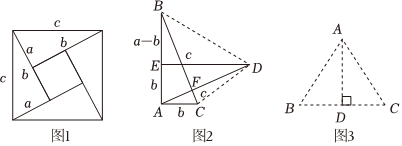23．【背景介紹】勾股定理是幾何學中的明珠，充滿著魅力．如圖1是著名的趙爽弦圖，由四個全等的直角三角形拼成，用它可以證明勾股定理，思路是大正方形的面積有兩種求法，一種是等于c²另一種是等于四個直角三角形與一個小正方形的面積之和，即
1
2
ab
×
4
+
（
b
-
a
）
2
從而得到等式
c
2
=
1
2
ab
×
4
+
（
b
-
a
）
2
化簡使得結論a²+b²=c²這里用兩種求法來表示同一個量從而得到等式或方程的方法，我們稱之為“雙求法”．
【方法運用】千百年來，人們對勾股定理的證明趨之若鶩，其中有著名的數學家，也有業余數學愛好者．向常春在2010年構造發現了一個新的證法：把兩個全等的Rt△ABC和Rt△DEA如圖2放置，其三邊長分別為a,b,c,∠BAC=∠DEA=90°顯然BC⊥AD．
（1）請用a,b,c分別表示出四邊形ABDC，梯形AEDC，△EBD的面積，再探究這三個圖形面積之間的關系，證明勾股定理a²+b²=c²；
【方法遷移】
（2）如圖3，在△ABC中，AD是BC邊上的高，AB=4，AC=5，BC=6，設BD=x,求x的值．
組卷：504引用：2難度：0.5
解析
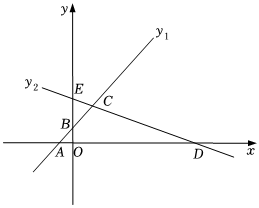24．如圖，在平面直角坐標系中，一次函數y₁=x+2的圖象與x軸，y軸分別交于點A，B，
y
2
=
-
1
3
x
+
b
的圖象與x軸，y軸分別交于點D，E，且兩個函數圖象相交于點C（m,5）．
（1）填空：m=
，b=
；
（2）求△ACD的面積；
（3）在線段AD上是否存在一點M，使得△ABM的面積與四邊形BMDC的面積比為4：21？若存在，請求出點M的坐標；若不存在，請說明理由．
（4）點P在線段AD上，連接CP，若△ACP是直角三角形，請直接寫出所有符合條件的點P坐標．
組卷：3127引用：7難度：0.3
解析