2022-2023學年江蘇省鎮江市丹陽高級中學九年級（上）期中數學試卷

一、選擇題（每題3分，共15分）

• 1．已知一個直角三角形的兩條直角邊恰好是方程2x²-9x+8=0的兩根，則此三角形的面積為（　　）

  A．1

  B．2

  C．3

  D．4
  組卷：93引用：4難度：0.7

  解析

• 2．已知△ABC，AB=10cm,BC=6cm,以點B為圓心，以BC為半徑畫圓⊙B，以點A為圓心，半徑為r,畫圓⊙A．已知⊙A與⊙B外離，則r的取值范圍為（　　）

  A．.0＜r≤4

  B．.0≤r≤4

  C．.0＜r＜4

  D．.0≤r＜4
  組卷：338引用：5難度：0.7

  解析

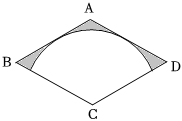• 3．如圖，在邊長為2的菱形ABCD中，∠BAD=120°，以點C為圓心畫弧，且與AB，AD邊相切，則圖中陰影部分的面積是（　　）

  A． 2 3 - 4 3 π

  B． 4 3 - 2 π

  C． 4 3 - 4 3 π

  D． 2 3 - π
  組卷：136引用：2難度：0.5

  解析

• 4．若x²-3x+1=0，則x⁴+

  1

  x

  4

  的個位數字是（　　）

  A．7

  B．8

  C．9

  D．10
  組卷：337引用：4難度：0.7

  解析

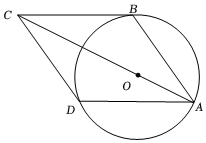• 5．如圖，?ABCD的三個頂點A、B、D均在⊙O上，且對角線AC過圓心O，BC與⊙O相切于點B，若⊙O的半徑為6，則?ABCD的面積為（　　）

  A．35

  B． 54 3

  C． 384 5

  D． 72 + 72 5 5
  組卷：588引用：3難度：0.6

  解析

二、填空題（本大題共12小題，每小題2分，共24分）

• 6．若在比例尺為1：1000000的地圖上，測得兩地的距離為1.5厘米，則這兩地的實際距離是

  千米．
  組卷：31引用：3難度：0.8

  解析

• 7．如果x：y=2：5，那么（x-y）：（x+y）=

  ．
  組卷：27引用：1難度：0.8

  解析

• 8．已知一元二次方程x²+3x+（a²+1）=0有一個根為x=-1，則a的值為

  ．
  組卷：305引用：4難度：0.7

  解析

三、解答題（本大題共九小題，計81分．解答時寫明演算步驟、證明過程或必要的文字說明）

• 25．【概念認識】
  與矩形一邊相切（切點不是頂點）且經過矩形的兩個頂點的圓叫做矩形的第Ⅰ類圓；與矩形兩邊相切（切點都不是頂點）且經過矩形的一個頂點的圓叫做矩形的第Ⅱ類圓．
  【初步理解】
  （1）如圖①～③，四邊形ABCD是矩形，⊙O₁和⊙O₂都與邊AD相切，⊙O₂與邊AB相切，⊙O₁和⊙O₃都經過點B，⊙O₃經過點D，3個圓都經過點C．在這3個圓中，是矩形ABCD的第Ⅰ類圓的是

  ，是矩形ABCD的第Ⅱ類圓的是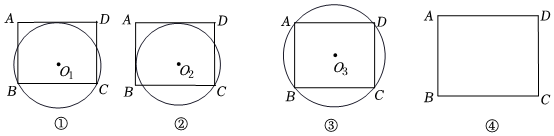

  ．
  【計算求解】
  （2）已知一個矩形的相鄰兩邊的長分別為4和6，直接寫出它的第Ⅰ類圓和第Ⅱ類圓的半徑長．
  【深入研究】
  （3）如圖④，已知矩形ABCD，用直尺和圓規作圖．（保留作圖痕跡，并寫出必要的文字說明）
  ①作它的1個第Ⅰ類圓；
  ②作它的1個第Ⅱ類圓．
  組卷：998引用：3難度：0.1

  解析

• 26．如圖，在平面直角坐標系xOy中，菱形OABC的頂點A在x軸的正半軸上，點C的坐標為（3，4），點D從原點O出發沿O→A→B勻速運動，到達點B時停止，點E從點A出發沿A→B→C隨D運動，且始終保持∠CDE=∠COA．設運動時間為t.
  
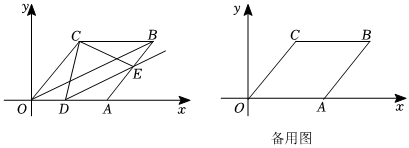
  （1）當DE∥OB時，求證：△OCD≌△BCE．
  （2）若點E在BC邊上，當△CDE為等腰三角形時，求BE的長．
  （3）若點D的運動速度為每秒1個單位，是否存在這樣的t,使得以點C，D，E為頂點的三角形與△OCD相似？若存在，直接寫出所有符合條件的t；若不存在，請說明理由．
  組卷：212引用：3難度：0.1

  解析