2021-2022學年貴州省遵義市桐梓縣私立達興中學八年級（下）第一次月考數學試卷

一、選擇題（本題共計12小題，每題4分，共計48分，）

• 1．下列四個數中，是負數的是（　　）

  A．|-2|

  B．（-2）2

  C．-（-2）

  D．-22
  組卷：12引用：2難度：0.9

  解析

• 2．下列運算正確的是（　　）

  A．（-m2n）2=m4n2	B．-m+m2=m
  C．-mn2?m3n=m4n3	D．（m3）2=m5
  組卷：162引用：2難度：0.6

  解析

• 3．截至2020年5月4日，海外新冠肺炎確診病例累計逾349.5萬例，數349.5萬用科學記數法表示為（　　）

  A．3.495×106

  B．34.95×105

  C．3.495×105

  D．0.3495×107
  組卷：105引用：4難度：0.9

  解析

• 4．下列各式中，不一定是非負數的是（　　）

  A． a 2

  B．|-a|

  C． 3 a

  D．（a-1）2
  組卷：19引用：1難度：0.8

  解析

• 5．以方程組

  y = - x + 2

  y = x - 1

  的解為坐標的點（x,y）在平面直角坐標系中的位置是（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  組卷：1320引用：107難度：0.9

  解析

• 6．下列圖形中既不是軸對稱圖形也不是中心對稱圖形的是（　　）

  A．

  B．

  C．

  D．
  組卷：13引用：3難度：0.9

  解析

• 7．若一個多邊形的內角和是外角和的3倍，則這個正多邊形的邊數是（　　）

  A．10

  B．9

  C．8

  D．6
  組卷：3283引用：20難度：0.9

  解析

• 8．函數

  y

  =

  5

  -

  x

  x

  -

  3

  自變量x的取值范圍是（　　）

  A．x≠3

  B．x≤5

  C．x≤5且x≠3

  D．x＜5且x≠3
  組卷：254引用：3難度：0.7

  解析

三、解答題（本題共計8小題，共計86分，）

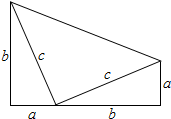• 23．如圖是美國總統Garfield于1876年給出的一種驗證勾股定理的辦法，你能利用它證明勾股定理嗎？請寫出你的證明過程．（提示：如圖三個三角形均是直角三角形）
  組卷：2273引用：21難度：0.7

  解析

• 24．課堂上同學們正在討論課本例題：如圖，一架2.5m長的梯子AB斜靠在豎直的墻AC上，BC的距離為0.7m,若梯子頂端下滑的距離為0.4m,則點B向外移動的距離為多少？
  同學甲：本題可以這樣來做
  解：在Rt△ABC中，BC=0.7m,AB=2.5m,根據勾股定理得：

  AC

  =

  2

  .

  5

  2

  -

  0

  .

  7

  2

  =

  2

  .

  4

  m

  ，則A₁C=

  m,
  又在Rt△A₁B₁C中，A₁B₁=2.5m,根據勾股定理得：B₁C=

  m,則B₁B=

  m.
  同學乙．我發現在本題答案中，梯子頂端下滑的距離AA₁比末端向外移動的距離BB₁小，說明在梯子下滑時，梯子頂端下滑的距離一定比末端向外移動的距離小．
  同學丙：不一定，我能舉個反例，比如，當梯子頂端下滑的距離為1.9m時，
  在Rt△ABC中，BC=0.7m,AB=2.5m,根據勾股定理得：AC=

  m,則A₁C=AC-AA₁=0.5m,
  又在Rt△A₁B₁C中，A₁B₁=2.5m,根據勾股定理得：B₁C=

  m,則B₁B=

  m.即：AA₁＞BB₁，
  老師．通過上面的討論，同學們發現有時AA₁大，有時BB₁大，那么有沒有可能正好AA₁=BB₁的情況存在呢？
  同學丁：有．當梯子頂端從A處下滑1.7m時，末端向外也移動1.7m.你認為他的說法正確嗎？說明理由．
  組卷：52引用：2難度：0.5

  解析