2022-2023學(xué)年河南省駐馬店市泌陽縣光亞學(xué)校九年級（上）第一次月考數(shù)學(xué)試卷

一、選擇題（每小題3分，共30分）下列各小題均有四個選項，其中只有一個是正確的正確答案的代號字母填在題后括號內(nèi).

• 1．下列二次根式中，是最簡二次根式的是（　　）

  A． 3

  B． 0 . 5

  C． 12

  D． 1 3
  組卷：436引用：9難度：0.9

  解析

• 2．將方程x²+9=6x改寫成ax²+bx+c=0（a≠0）的形式，則a,b,c的值分別為（　　）

  A．0，6，9

  B．0，6，-9

  C．1，-6，9

  D．1，-6，-9
  組卷：50引用：1難度：0.9

  解析

• 3．若代數(shù)式

  1

  x

  +

  1

  有意義，則實數(shù)x的取值范圍是（　　）

  A．x≠1

  B．x≥0

  C．x≥-1

  D．x≥0且x≠-1
  組卷：180引用：1難度：0.9

  解析

• 4．用配方法解方程x²-4x+3=0時，方程可變形為（　　）

  A．（x-2）2=1

  B．（x-2）2=-1

  C．（x-2）2=9

  D．（x-2）2=-9
  組卷：62引用：4難度：0.6

  解析

• 5．下列運算正確的是（　　）

  A． 2 + 3 = 5

  B．2 3 - 3 =2

  C． 4 × 9 = - 4 × - 9

  D． 6 ÷ 3 = 2
  組卷：81引用：3難度：0.7

  解析

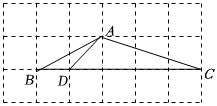• 6．如圖，△ABD和△ABC的頂點均在邊長為1的小正方形網(wǎng)格格點上，則∠BAC的度數(shù)為（　　）

  A．115°

  B．135°

  C．150°

  D．無法計算
  組卷：231引用：5難度：0.6

  解析

• 7．一元二次方程（x+2）（x-4）=-9的根的情況是（　　）

  A．有兩個不相等的實數(shù)根	B．有兩個相等的實數(shù)根
  C．只有一個實數(shù)根	D．沒有實數(shù)根
  組卷：41引用：1難度：0.6

  解析

三、解答題（本大題共8個小題，共75分）

• 22．閱讀理解：已知x=

  2

  +1，求代數(shù)式x²-2x-5的值．王紅的做法是：根據(jù)x=

  2

  +1得（x-1）²=2，∴x²-2x+1=2，得：x²-2x=1．把x²-2x作為整體代入：得x²-2x-5=1-5=-4．即：把已知條件適當(dāng)變形，再整體代入解決問題．
  請你用上述方法解決下面問題：
  （1）已知x=

  3

  -2，求代數(shù)式x²+4x-5的值；
  （2）已知x=

  5

  -

  1

  2

  ，求代數(shù)式x³+x²+1的值．
  組卷：379引用：2難度：0.7

  解析

• 23．

  倍長中線（Method of times the length of line） 倍長中線的意思是：延長邊上（不一定是底邊）的中線，使所延長部分與中線相等，然后往往需要連接相應(yīng)的頂點，則對應(yīng)角對應(yīng)邊都對應(yīng)相等，此法常用于構(gòu)造全等三角形，利用中線的性質(zhì)、輔助線、對頂角一般用“SAS”證明對應(yīng)邊之間的關(guān)系．

  請用倍長中線法解答下面問題：在△ABC中，∠ACB=90°，BD是AC邊上的中線，點E為射線BC上一動點．
  （1）問題發(fā)現(xiàn)
  如圖1，點E在BC上，BE：CE=1：2，BD與AE相交于點P，延長BD至點F，使得BD=DF，連接AF，求

  AP

  PE

  的值．
  王林同學(xué)根據(jù)題意寫出了如下不完整的求解過程，請補(bǔ)全其過程．
  

  解：設(shè)BE=k,則CE= ； ∵BD是AC邊上的中線， ∴AD=CD； ∵在△BCD和△FAD中， CD = AD ∠ BDC =∠ FDA BD = FD ∴△BCD≌△FAD（ ） ∴ = ， ∴BC∥FA；∴BC=FA=3k； 又∵BC∥FA， ∴△BPE∽△FPA； ∴ AP PE = AF BE = ．

  （2）類比探究
  如圖2，點E在BC的延長線上，AE與BD的延長線交于點P，CE：BC=1：3，求

  AP

  PE

  的值．
  （3）拓展延伸
  在（2）的探究結(jié)論下，若BC=4，AC=6，求BP的長．
  
  組卷：282引用：2難度：0.3

  解析