當前位置：試卷中心 > 試卷詳情

2022-2023學年湖南省株洲市建寧實驗中學九年級（上）期末數學試卷

發布：2024/4/20 14:35:0

一、選擇題（本大題共10小題，每小題有且只有一個正確答案，每小題4分，共40分）

1．將方程（x-1）²=6化成一元二次方程的一般形式，正確的是（　　）
A．x²-2x+5=0 B．x²-2x-5=0 C．x²+2x-5=0 D．x²+2x+5=0
組卷：540引用：7難度：0.9
解析
2．點A（-3，y₁）、B（-1，y₂）在反比例函數
y
=
6
x
的圖象上，則y₁、y₂的大小關系是（　　）
A．y₁＜y₂ B．y₂＜y₁ C．y₁=y₂ D．不能確定
組卷：82引用：2難度：0.7
解析
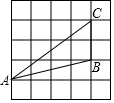3．如圖，將△ABC放在每個小正方形的邊長為1的網格中，點A，B，C均在格點上，則tanC的值是（　　）
A．2 B．
4
3
C．1 D．
3
4
組卷：4236引用：12難度：0.6
解析
4．某招聘考試分筆試和面試兩種，其中按筆試60%、面試40%計算加權平均數，作為總成績．小明筆試成績90分，面試85分，則小明的總成績是（　　）
A．88分 B．87.5分 C．87分 D．86分
組卷：104引用：4難度：0.7
解析
5．在△ABC中，∠ABC=90°，用直尺和圓規在AC上確定點D，使△ABD∽△BCD，如下四個尺規作圖，正確的是（　　）
A．（作一個角的平分線） B．（作線段的垂直平分線）
C．（作高） D．（作等腰三角形）
組卷：307引用：5難度：0.6
解析
6．在Rt△ACB中，∠C=90°，AB=8，sinA=
3
4
，則BC的長為（　　）
A．6 B．7.5 C．8 D．12.5
組卷：1296引用：16難度：0.7
解析
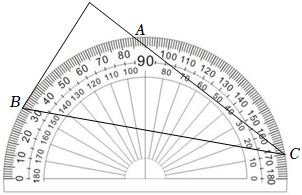7．將量角器按如圖所示的方式放置在三角形紙板上，使點C在半圓上．點A，B的讀數分別為86°，30°，則∠ACB的度數是（　　）
A．28° B．30° C．36° D．56°
組卷：2951引用：27難度：0.5
解析
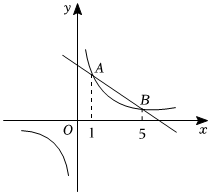8．如圖，直線y=k₁x+b與雙曲線
y
=
k
2
x
交于A、B兩點，其橫坐標分別為1和5，則不等式
k
1
x
+
b
＜
k
2
x
的解集是（　　）
A．1＜x＜5 B．x＞5或x＜1 C．x＞5或0＜x＜1 D．1≤x≤5
組卷：806引用：5難度：0.7
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

三、解答題（本大題共8小題，共78分）

25．如圖1，平面直角坐標系xOy中，A（4，3），反比例函數y=
k
x
（k＞0）的圖象分別交矩形ABOC的兩邊AC，AB于E、F兩點（E、F不與A重合），沿著EF將矩形ABOC折疊使A、D兩點重合．
（1）AE=
（用含有k的代數式表示）；
（2）如圖2，當點D恰好落在矩形ABOC的對角線BC上時，求CE的長度；
（3）若折疊后，△ABD是等腰三角形，求此時點D的坐標．
組卷：3206引用：11難度：0.1
解析
26．閱讀理解：
材料1：對于一個關于x的二次三項式ax²+bx+c（a≠0），除了可以利用配方法求該多項式的取值范圍外，愛思考的小川同學還想到了其他的方法：比如先令ax²+bx+c=y（a≠0），然后移項可得：ax²+bx+（c-y）=0，再利用一元二次方程根的判別式來確定y的取值范圍，請仔細閱讀下面的例子：
例：求x²+2x+5的取值范圍；
解：令x²+2x+5=y
∴x²+2x+（5-y）=0
∴Δ=4-4×（5-y）≥0
∴y≥4
∴x²+2x+5≥4；
材料2：在學習完一元二次方程的解法后，愛思考的小川同學又想到仿造一元二次方程的解法來解決一元二次不等式的解集問題，他的具體做法如下：
若關于x的一元二次方程ax²+bx+c=0（a＞0）有兩個不相等的實數根x₁、x₂（x₁＞x₂）
則關于x的一元二次不等式ax²+bx+c≥0（a＞0）的解集為：x≥x₁或x≤x₂
則關于x的一元二次不等式ax²+bx+c≤0（a＞0）的解集為：x₂≤x≤x₁；
材料3：若關于x的一元二次方程ax²+bx+c=0（a≠0）有兩個不相等的實數根x₁，x₂；
則x₁+x₂=-
b
a
；x₁?x₂=
c
a
，我們稱之為韋達定理；
請根據上述材料，解答下列問題：
（1）若關于x的二次三項式x²+ax+3（a為常數）的最小值為-7，則a=
．
（2）求出代數式
x
2
-
4
x
+
2
2
x
-
1
的取值范圍．
（3）若關于x的代數式
2
bx
+
a
x
2
-
2
x
+
3
（其中a、b為常數，且ab≠0）的最小值為-2，最大值為4，請求出滿足條件的a、b的值．
組卷：496引用：3難度：0.4
解析