2022-2023學(xué)年山東省淄博市部分學(xué)校高一（下）期中數(shù)學(xué)試卷

一、單選題（每題5分，共40分）

• 1．將120°轉(zhuǎn)化為弧度為（　　）

  A． 5 π 6

  B． 2 π 3

  C． 5 6

  D． 2 3
  組卷：486引用：3難度：0.9

  解析

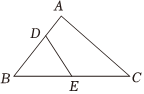• 2．如圖所示的△ABC中，點(diǎn)D是線段AB上靠近A的三等分點(diǎn)，點(diǎn)E是線段BC的中點(diǎn)，則

  DE

  =（　　）

  A． - 1 6 AB - 1 2 AC

  B． 1 6 AB + 1 2 AC

  C． 1 2 AC - 1 6 AB

  D． 5 6 AB + 1 2 AC
  組卷：112引用：2難度：0.8

  解析

• 3．化簡(jiǎn)sin347°cos148°+sin77°cos58°的值為（　　）

  A． 3 2

  B． - 3 2

  C． 1 2

  D． 2 2
  組卷：656引用：2難度：0.7

  解析

• 4．已知向量

  a

  、

  b

  不共線，且

  c

  =

  x

  a

  +

  b

  ，

  d

  =

  a

  +

  （

  2

  x

  -

  1

  ）

  b

  ，若

  c

  與

  d

  共線，則實(shí)數(shù)x的值為（　　）

  A．1

  B． - 1 2

  C．1或 - 1 2

  D．-1或 - 1 2
  組卷：624引用：10難度：0.7

  解析

• 5．設(shè)a=

  3

  2

  cos

  6

  °

  -

  1

  2

  sin

  6

  °

  ，b=

  2

  tan

  27

  °

  1

  -

  tan

  2

  27

  °

  ，c=

  1

  -

  cos

  110

  °

  2

  ，則有（　　）

  A．c＜b＜a

  B．a(chǎn)＜b＜c

  C．a(chǎn)＜c＜b

  D．b＜c＜a
  組卷：237引用：3難度：0.7

  解析

• 6．已知扇形面積為

  3

  π

  8

  ，半徑是1，則扇形的周長(zhǎng)是（　　）

  A． 3 π 16 + 1

  B． 3 π 8 + 2

  C． 3 π 4 + 2

  D． 3 π 2 + 1
  組卷：262引用：4難度：0.9

  解析

• 7．已知角θ與φ都是任意角，若滿足

  θ

  +

  φ

  =

  π

  2

  ，則稱θ與φ“廣義互余”．已知

  sin

  （

  π

  +

  α

  ）

  =

  -

  1

  4

  ，下列角β中，可能與角α“廣義互余”的是（　　）

  A． sinβ = 1 4	B． cos （ π - β ） = 1 4
  C． tanβ = 15 15	D． cos （ 2 π - β ） = 1 4
  組卷：312引用：4難度：0.7

  解析

四、解答題（共70分）

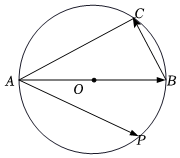• 21．如圖，AB是半徑為1的圓O的直徑，點(diǎn)C為圓周上一點(diǎn)，且∠ABC=60°，點(diǎn)P為圓周上一動(dòng)點(diǎn)．
  （Ⅰ）求

  AB

  ?

  BC

  的值；
  （Ⅱ）求

  AB

  ?

  AP

  的最大值．
  組卷：183引用：3難度：0.8

  解析

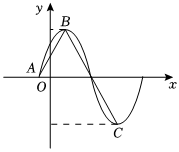• 22．已知函數(shù)

  f

  （

  x

  ）

  =

  4

  cosωx

  ?

  cos

  （

  ωx

  -

  π

  3

  ）

  -

  1

  （

  ω

  ＞

  0

  ）

  的部分圖像如圖所示，若

  AB

  ?

  BC

  =

  π

  2

  8

  -

  8

  ，B，C分別為最高點(diǎn)與最低點(diǎn)．
  （1）求函數(shù)f（x）的解析式；
  （2）若函數(shù)y=f（x）-m在

  [

  0

  ，

  13

  π

  12

  ]

  上有且僅有三個(gè)不同的零點(diǎn)x₁，x₂，x₃，（x₁＜x₂＜x₃），求實(shí)數(shù)m的取值范圍，并求出cos（x₁+2x₂+x₃）的值．
  組卷：724引用：3難度：0.3

  解析