2022-2023學年北京市西城區三帆中學八年級（上）期中數學試卷

一.選擇題（本題共16分，每小題2分）

• 1．對稱現象無處不在，下列漢字是軸對稱圖形的是（　　）

  A．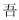

  B．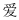

  C．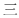

  D．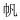
  組卷：4引用：2難度：0.8

  解析

• 2．下列運算正確的是（　　）

  A．m2?m3=m6	B．（m3）2=m6
  C．m（-m+2）=m2+2m	D．m2+m3=2m6
  組卷：27引用：2難度：0.8

  解析

• 3．若一個三角形的兩邊長分別為3cm、7cm,則它的第三邊的長可能是（　　）

  A．2cm

  B．3cm

  C．8cm

  D．11cm
  組卷：125引用：4難度：0.7

  解析

• 4．下列說法錯誤的是（　　）

  A．直角三角形兩銳角互余

  B．有三組角分別相等的兩個三角形全等

  C．與線段兩個端點距離相等的點在這條線段的垂直平分線上

  D．角平分線上的點到角兩邊的距離相等
  組卷：10引用：2難度：0.5

  解析

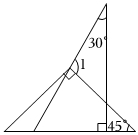• 5．一副三角板按如圖方式放置，則∠1的度數是（　　）

  A．105°

  B．135°

  C．150°

  D．165°
  組卷：55引用：2難度：0.5

  解析

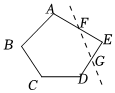• 6．如圖，將一個五邊形ABCDE沿虛線裁去一個角后得到的多邊形ABCDGF的內角和為（　　）

  A．180°

  B．360°

  C．540°

  D．720°
  組卷：188引用：4難度：0.8

  解析

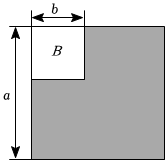• 7．如圖，將一個邊長為b的正方形B放在一個邊長為a的大正方形A中，則陰影部分的面積計算可以用等式表示為（　　）

  A．（a-b）b+a（a-b）=a2-b2	B．（a+b）2=a2+2ab+b2
  C．（a-b）2=a2-2ab+b2	D．a（a-b）=a2-ab
  組卷：57引用：4難度：0.8

  解析

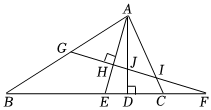• 8．如圖，在△ABC中，AD，AE分別是△ABC的高線和角平分線，FG⊥AE于點H，交AD于點J，下列結論：①∠DAE=∠F；②∠FJD=∠CAE+∠B；③∠ACB=∠AGH；④∠F=

  1

  2

  （∠ACB-∠B）中，正確的有（　　）

  A．①②

  B．①②④

  C．②③④

  D．①④
  組卷：99引用：3難度：0.5

  解析

四、解答題（本題共52分，第19-23題每題6分，24、25題每題7分，26題8分）

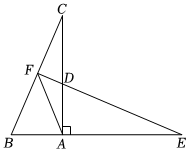• 25．已知：如圖，在△ABC中，∠CAB=90°，點D為AC上的一點，AD=AB，點E為BA延長線上一點且AE=AC，連接ED并延長交BC于點F，連結AF．
  （1）求證：∠FCA=∠AEF；
  （2）作A點關于BC的對稱點M，分別連接AM，FM．
  ①依題意補全圖形；
  ②用等式表示EF，CF，AM之間的數量關系并證明．
  組卷：550引用：4難度：0.5

  解析

• 26．給出如下定義：如圖1，已知∠RST=90°，∠PMQ=45°，直線l垂直平分線段MS，若∠PMQ關于直線l的軸對稱圖形G完全落在∠RST內部（G的兩邊不與∠RST的邊重合），則稱∠PMQ是∠RST的內含對稱半角．
  在平面直角坐標系xOy中，正方形OABC四個頂點的坐標分別為O（0，0），A（0，4），B（4，4），C（4，0），M（m,0）為x軸負半軸上一點，射線MP繞點M逆時針旋轉45°到達MQ的位置，形成∠PMQ．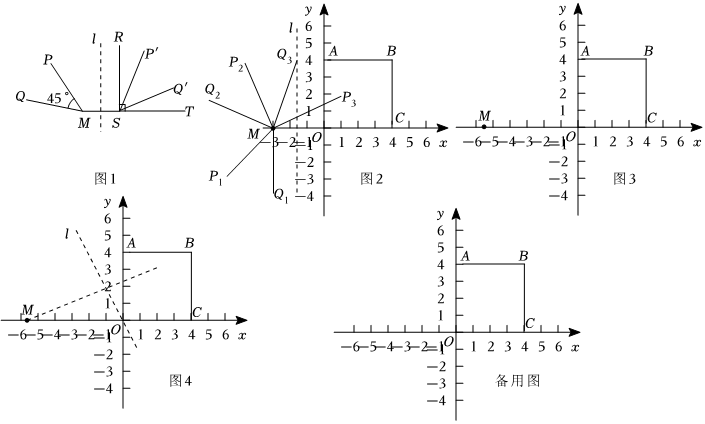
  
  （1）如圖2，直線l垂直平分線段OM，∠P₁MQ₁=∠P₂MQ₂=∠P₃MQ₃=45°，其中

  是∠AOC的內含對稱半角．
  （2）若∠PMQ是∠OCB的內含對稱半角，請在圖3中畫出符合題意的一個∠PMQ．
  （3）如圖4，若直線l經過原點，設∠PMO=α，當α為何值時∠PMQ是∠ABC的內含對稱半角？請直接寫出α的范圍：

  ；
  （4）當m為何值時，∠OAB的內含對稱半角（M點除外）位于x軸下方？請直接寫出m的范圍：

  ．
  組卷：302引用：3難度：0.2

  解析