2022-2023學年湖南省長沙一中雙語實驗學校九年級（上）第三次月考數學試卷

一、單選題（共30分）

• 1．下列各式中，結果是2022的是（　　）

  A．-（+2022）

  B．-（-2022）

  C．-|-2022|

  D．-|+2022|
  組卷：20引用：3難度：0.8

  解析

• 2．多項式3x²-8yx²-3xy³+1是（　　）

  A．三次四項式

  B．三次三項式

  C．四次四項式

  D．四次三項式
  組卷：31引用：1難度：0.7

  解析

• 3．如圖，四個幾何體分別為四棱錐、三棱柱、圓柱體和長方體，這四個幾何體中截面可能是圓形的幾何體是（　　）

  A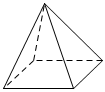． 四棱錐

  B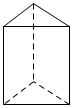． 三棱柱

  C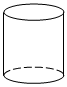． 圓柱體

  D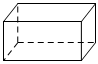． 長方體
  組卷：172引用：3難度：0.7

  解析

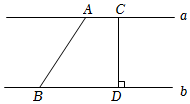• 4．如圖，直線a∥b,則直線a,b之間的距離是（　　）

  A．線段AB	B．線段AB的長度
  C．線段CD	D．線段CD的長度
  組卷：362引用：4難度：0.7

  解析

• 5．下列是方程2x+y=7的解的是（　　）

  A． x = - 1 y = 5

  B． x = 1 y = 5

  C． x = 3 y = 4

  D． x = 4 y = 3
  組卷：601引用：4難度：0.7

  解析

• 6．下列說法正確的是（　　）

  A．a不是負數，則a＞0	B．m不小于-1，則m＞-1
  C．a+b是負數，則a+b＜0	D．b是不大于0的數，則b＜0
  組卷：141引用：5難度：0.8

  解析

• 7．下列長度的三條線段，首尾相連能組成三角形的是（　　）

  A．2cm、2cm、4cm	B．2cm、4cm、6cm
  C．4cm、10cm、4cm	D．3cm、4cm、5cm
  組卷：57引用：3難度：0.8

  解析

• 8．下列命題錯誤的是（　　）

  A．三角形的三條高交于一點

  B．三角形的三條中線都在三角形內部

  C．直角三角形的三條高交于一點，且交點在直角頂點處

  D．三角形的三條角平分線交于一點，且這個交點到三角形三邊的距離相等
  組卷：103引用：3難度：0.6

  解析

三、解答題（共72分）

• 24．定義：若兩個函數的圖象關于某一點Q中心對稱，則稱這兩個函數關于點Q互為“對稱函數”．例如，函數y=x²與y=-x²關于原點O互為“對稱函數”．
  （1）函數y=-x+1關于原點O的“對稱函數”的函數解析式為

  ，函數y=（x-2）²-1關于原點O的“對稱函數”的函數解析式為

  ；
  （2）已知函數y=x²-2x與函數G關于點Q（0，1）互為“對稱函數”，若函數y=x²-2x與函數G的函數值y都隨自變量x的增大而減小，求x的取值范圍；
  （3）已知點A（0，1），點B（4，1），點C（2，0），二次函數y=ax²-2ax-3a（a＞0），與函數N關于點C互為“對稱函數”，將二次函數y=ax²-2ax-3a（a＞0）與函數N的圖象組成的圖形記為W，若圖形W與線段AB恰有2個公共點，直接寫出a的取值范圍．
  組卷：690引用：3難度：0.1

  解析

• 25．已知△ABC為等腰直角三角形，∠CAB=90°，點D為平面內的一動點，滿足CD=CA，將線段AD繞A點按逆時針方向旋轉90°得到線段AE，連接CE．
  
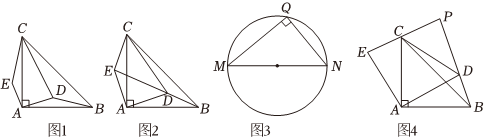
  （1）當點D在△ABC內部時．①如圖1，求證：△AEC≌△ADB；②如圖2，當點E，D，B在同一直線上時，若

  AB

  =

  2

  10

  ，求CE的長；
  （2）閱讀材料：如圖3，已知線段MN為定長，若以MN為斜邊作Rt△MQN，其中∠Q=90°，根據直角三角形的性質“直角三角形斜邊上的中線等于斜邊的一半”，則以MN為斜邊的直角三角形的直角頂點Q的軌跡是：以線段MN中點為圓心，

  1

  2

  MN

  長為半徑的圓（M，N兩點除外）．如圖4，已知AB=6．若直線CE與直線BD相交于點P．點G為線段BC上的一動點，將線段AG繞點A按順時針方向旋轉90°得到AG'，連接PG'，求PG'長度的取值范圍．
  組卷：191引用：3難度：0.2

  解析