2021-2022學年江蘇省蘇州市常熟中學高一（下）調研數學試卷（3月份）

一、單項選擇題：本題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．

• 1．如圖所示，在△ABC中，點D在線段BC上，且BD=3DC，若

  AD

  =

  λ

  AB

  +

  μ

  AC

  ，則

  λ

  μ

  =（　　）

  A． 1 2

  B． 1 3

  C．2

  D． 2 3
  組卷：700引用：6難度：0.6

  解析

• 2．函數f（x）=

  2

  sinx-tanx在x∈（-

  π

  2

  ，

  π

  2

  ）時的圖象大致是（　　）

  A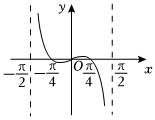．	B．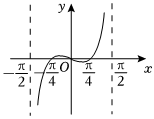
  C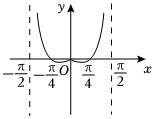．	D．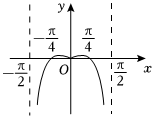
  組卷：91引用：3難度：0.8

  解析

• 3．三角形ABC所在平面內一點P滿足

  PA

  ?

  PB

  =

  PB

  ?

  PC

  =

  PC

  ?

  PA

  ，那么P是三角形ABC的（　　）

  A．重心

  B．垂心

  C．外心

  D．內心
  組卷：110引用：4難度：0.9

  解析

• 4．已知將函數f（x）=cos2x的曲線向左平移

  π

  6

  個單位長度后得到曲線y=g（x），則函數y=g（x）的單調遞增區間是（　　）

  A． [ kπ - π 12 ， kπ + 5 π 12 ] （ k ∈ Z ）	B． [ kπ - 7 π 12 ， kπ - π 12 ] （ k ∈ Z ）
  C． [ kπ - 2 π 3 ， kπ - π 6 ] （ k ∈ Z ）	D． [ kπ - π 6 ， kπ + π 3 ] （ k ∈ Z ）
  組卷：108引用：1難度：0.7

  解析

• 5．已知a,b,c分別為△ABC三個內角A，B，C的對邊，且acosC+bcosA=b,則△ABC是（　　）

  A．等腰三角形	B．直角三角形
  C．等腰直角三角形	D．等腰或直角三角形
  組卷：649引用：12難度：0.7

  解析

• 6．已知

  AB

  ⊥

  AC

  ，

  |

  AB

  |

  =

  1

  t

  ，

  |

  AC

  |

  =

  t

  ，若P點是△ABC所在平面內一點，且

  AP

  =

  AB

  |

  AB

  |

  +

  4

  AC

  |

  AC

  |

  ，則

  PB

  ?

  PC

  的最大值等于（　　）

  A．13

  B．15

  C．19

  D．21
  組卷：6851引用：54難度：0.7

  解析

• 7．已知函數f（x）=4sin²x+asinx+1在區間[0，π]上有4個不同的零點，則實數a的取值范圍是（　　）

  A．-8＜a＜-4	B．-5＜a＜-4
  C．a＜-4	D．-5＜a＜-4或a＞4
  組卷：85引用：1難度：0.5

  解析

四、解答題：本大題共6小題，共70分．解答應寫出文字說明、證明過程或演算步驟．

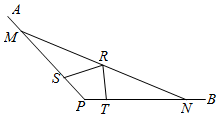• 21．由于2020年1月份國內疫情暴發，經濟活動大范圍停頓，餐飲業受到重大影響．6月初政府在個別地區推行地攤經濟、小店經濟以刺激消費和促進就業．某商場經營者吳某準備在商場門前“擺地攤”，經營冷飲生意．已知該商場門前是一塊角形區域，如圖所示，其中∠APB=120°，且在該區域內點R處有一個路燈，經測量點R到區域邊界PA，PB的距離分別為RS=4m,RT=6m,（m為長度單位）．吳某準備過點R修建一條長椅MN（點M，N分別落在PA，PB上，長椅的寬度及路燈的粗細忽略不計），以供購買冷飲的人休息．
  （1）求線段PR的長；
  （2）為優化經營面積，當PM等于多少時，該三角形PMN區域面積最小？并求出面積的最小值．
  組卷：109引用：3難度：0.5

  解析

• 22．已知函數f（x）=asinx+bcosx+csinxcosx+1（a,b,c∈R）．
  （1）當a=b=c=1時，求f（x）的值域；
  （2）當a=1，c=0時，設g（x）=f（x）-1，且g（x）關于直線

  x

  =

  π

  6

  對稱，當x∈[0，π]時，方程g（x）-m=0恰有兩個不等的實根，求實數m的取值范圍；
  （3）當

  a

  =

  3

  ，b=1，c=0時，若實數m,n,p使得mf（x）+nf（x-p）=1對任意實數x恒成立，求

  cosp

  3

  m

  +

  n

  的值．
  組卷：121引用：2難度：0.5

  解析