2022-2023學年天津市寧河區蘆臺一中高三（上）期末數學試卷

一、選擇題（每小題5分，共45分，在每小題所給的四個選項中，只有一項符合題目要求）

• 1．已知集合A={-1，0，1，2}，B={x|y=log₂x}，則A∩B=（　　）

  A．{-1，1}

  B．{1，2}

  C．{0，2}

  D．{0，1，2}
  組卷：62引用：3難度：0.9

  解析

• 2．“a+b＞2c”是“a＞b＞c”的（　　）

  A．充要條件	B．必要不充分條件
  C．充分不必要條件	D．既不充分也不必要條件
  組卷：89引用：2難度：0.8

  解析

• 3．函數

  f

  （

  x

  ）

  =

  x

  3

  +

  x

  3

  x

  +

  3

  -

  x

  的部分圖象可能是（　　）

  A．

  B．

  C．

  D．
  組卷：272引用：7難度：0.9

  解析

• 4．設

  a

  =

  lo

  g

  2

  2

  π

  ，

  b

  =

  202

  2

  0

  .

  8

  ，

  c

  =

  202

  3

  -

  0

  .

  67

  ，則（　　）

  A．c＜b＜a

  B．a＜c＜b

  C．a＜b＜c

  D．b＜c＜a
  組卷：332引用：5難度：0.7

  解析

• 5．已知雙曲線

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  0

  ，

  b

  ＞

  0

  ）

  的右焦點F與拋物線y²=8x的焦點重合，拋物線準線與一條漸近線交于點

  A

  （

  m

  ,-

  2

  3

  ）

  ，則雙曲線的方程為（　　）

  A． x 2 12 - y 2 4 = 1

  B． x 2 4 - y 2 12 = 1

  C． x 2 3 - y 2 = 1

  D． x 2 - y 2 3 = 1
  組卷：258引用：6難度：0.5

  解析

• 6．已知直線：l：x-y+3=0被圓C：（x-a）²+（y-2）²=4（a＞0）截得的弦長為

  2

  2

  ，則點（-a,a-1）與圓上點的距離最大值為（　　）

  A． 2 2 + 2

  B． 2 2 - 2

  C．2

  D．4
  組卷：284引用：3難度：0.5

  解析

三、解答題：共5小題，75分．解答應寫出文字說明，證明過程或演算步驟．

• 19．已知橢圓C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =1（a＞b＞0）的離心率為

  2

  2

  ，短軸長為2

  2

  ．
  （Ⅰ）求C的方程；
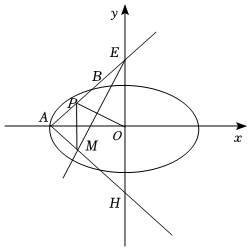
  （Ⅱ）如圖，經過橢圓左頂點A且斜率為k（k≠0）直線l與C交于A，B兩點，交y軸于點E，點P為線段AB的中點，若點E關于x軸的對稱點為H，過點E作與OP（O為坐標原點）垂直的直線交直線AH于點M，且△APM面積為

  2

  3

  ，求k的值．
  組卷：418引用：5難度：0.5

  解析

• 20．設函數f（x）=xe^kx+a,f′（x）為f（x）的導函數．
  （1）當k=-1時，
  ①若函數f（x）的最大值為0，求實數a的值；
  ②若存在實數x＞0，使得不等式f（x）≥x-lnx成立，求實數a的取值范圍．
  （2）當k=1時，設g（x）=f′（x），若g（x₁）=g（x₂），其中x₁≠x₂，證明：x₁x₂＞4．
  組卷：110引用：2難度：0.3

  解析