當前位置：試卷中心 > 試卷詳情

2022-2023學年四川省成都外國語學校高二（下）期中數學試卷（理科）

發布：2024/11/21 9:0:2

1．已知i為虛數單位，復數
z
=
1
-
i
i
，則|z|=（　　）
A．1 B．
2
C．
3
D．2
組卷：44引用：4難度：0.8
解析
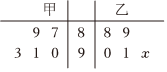2．如圖莖葉圖記錄了甲乙兩位射箭運動員的5次比賽成績（單位：環），若兩位運動員平均成績相同，則運動員乙成績的方差為（　　）
A．2 B．3 C．9 D．16
組卷：63引用：9難度：0.7
解析
3．已知雙曲線
C
：
x
2
a
2
-
y
2
b
2
=
1
（
a
＞
0
，
b
＞
0
）
的一條漸近線方程為2x-y=0，則雙曲線C的離心率為（　　）
A．2 B．
2
C．
3
D．
5
組卷：258引用：5難度：0.8
解析
4．已知m,n表示兩條不同的直線，α表示平面．下列說法正確的是（　　）
A．若m∥α，n∥α，則m∥n B．若m⊥α，n⊥α，則m∥n
C．若m⊥α，m⊥n,則n∥α D．若m∥α，m⊥n,則n⊥α
組卷：1144引用：14難度：0.6
解析
5．“m=4”是“直線（3m-4）x+4y-2=0與直線mx+2y-2=0平行”的（　　）
A．充分而不必要條件 B．必要而不充分條件
C．充要條件 D．既不充分也不必要條件
組卷：74引用：4難度：0.7
解析
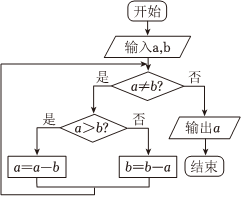6．執行該程序框圖，若輸入的a,b分別為35、28，則輸出的a=（　　）
A．1 B．7 C．14 D．28
組卷：9引用：4難度：0.8
解析
7．函數f（x）=（x²-2x）e^x的圖像大致是（　　）
A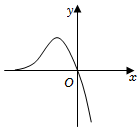． B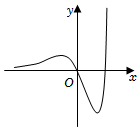． C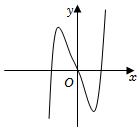． D．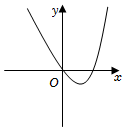
組卷：351引用：29難度：0.8
解析

21．已知橢圓
C
：
x
2
a
2
+
y
2
b
2
=
1
（
a
＞
b
＞
0
）
的離心率為
3
2
，左、右焦點分別為F₁，F₂，P為C的上頂點，且△PF₁F₂的周長為
4
+
2
3
．
（Ⅰ）求橢圓C的方程；
（Ⅱ）設過定點M（0，2）的直線l與橢圓C交于不同的兩點A、B，且∠AOB為銳角（其中O為坐標原點），求直線l的斜率k的取值范圍．
組卷：651引用：6難度：0.5
解析
22．已知函數f（x）=xlnx-ax²+a.
（1）若f（x）≤a,求a的取值范圍；
（2）若f（x）存在唯一的極小值點x₀，求a的取值范圍，并證明2a-1＜f（x₀）＜0．
組卷：137引用：2難度：0.3
解析

A．若m∥α，n∥α，則m∥n	B．若m⊥α，n⊥α，則m∥n
C．若m⊥α，m⊥n,則n∥α	D．若m∥α，m⊥n,則n⊥α

A．充分而不必要條件	B．必要而不充分條件
C．充要條件	D．既不充分也不必要條件

1．已知i為虛數單位，復數z=1-ii，則|z|=（ ）