2023年重慶市南開中學高考數學第四次質檢試卷

一、單項選擇題：本題共8小題．每小題5分，共40分．在每小題給出的四個選項中，只有一項符合題目要求．

• 1．已知復數z滿足z（1+i）=2i,其中i為虛數單位，則復數z的模|z|=（　　）

  A．1

  B． 2

  C．2

  D． 2 2
  組卷：205引用：8難度：0.8

  解析

• 2．已知集合A={-1，0}，B={1，2}，則集合C={z|z=x²+y²，x∈A，y∈B}的真子集個數為（　　）

  A．7

  B．8

  C．15

  D．16
  組卷：217引用：3難度：0.8

  解析

• 3．已知直線l₁：（m-2）x-3y-1=0與直線l₂：mx+（m+2）y+1=0相互平行，則實數m的值是（　　）

  A．-4

  B．1

  C．-1

  D．6
  組卷：526引用：13難度：0.7

  解析

• 4．公元五世紀，數學家祖沖之估計圓周率π的范圍是：3.1415926＜π＜3.1415927，為紀念祖沖之在圓周率方面的成就，把3.1415926稱為“祖率”，這是中國數學的偉大成就．小明是個數學迷，他在設置手機的數字密碼時，打算將圓周率的前6位數字3，1，4，1，5，9進行某種排列得到密碼．如果排列時要求兩個1不相鄰，那么小明可以設置的不同密碼有（　　）個

  A．240

  B．360

  C．600

  D．720
  組卷：314引用：11難度：0.8

  解析

• 5．已知函數

  f

  （

  x

  ）

  =

  ln

  （

  x

  2

  +

  1

  -

  x

  ）

  +

  1

  ，正實數a,b滿足f（2a）+f（b-4）=2，則

  4

  b

  a

  +

  a

  2

  ab

  +

  b

  2

  的最小值為（　　）

  A．1

  B．2

  C．4

  D． 65 8
  組卷：383引用：4難度：0.6

  解析

• 6．已知函數f（x）=

  x + 1 ， x ≤ 0

  | x - 1 x | ， x ＞ 0

  ，若關于x的方程f²（x）+（m-4）f（x）+2（2-m）=0有五個不同的實數根，則實數m的取值范圍是（　　）

  A．[1，3）

  B．（0，2）

  C．[1，2）

  D．（0，1）
  組卷：483引用：5難度：0.5

  解析

• 7．已知點P為拋物線y²=2px（p＞0）上一動點，點Q為圓C：（x+1）²+（y-4）²=1上一動點，點F為拋物線的焦點，點P到y軸的距離為d,若|PQ|+d的最小值為2，則p=（　　）

  A． p = 1 2

  B．p=1

  C．p=2

  D．p=4
  組卷：234引用：6難度：0.6

  解析

四、解答題：本題共6小題，共70分．解答應寫出文字說明、證明過程或演算步驟．

• 21．已知函數f（x）=e^x（x-2a）+ax+2，a∈R．
  （1）當a=1時，求曲線f（x）在點（1，f（1））處的切線方程；
  （2）若不等式f（x）≥0對?x≥0恒成立，求實數a的范圍；
  （3）證明：當

  n

  ∈

  N

  *

  ，

  1

  +

  1

  2

  +

  1

  3

  +

  ?

  +

  1

  n

  ＜

  ln

  （

  2

  n

  +

  1

  ）

  ．
  組卷：145引用：3難度：0.4

  解析

• 22．已知橢圓

  C

  1

  ：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

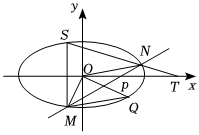  的左右焦點分別為F₁，F₂，右頂點為A，上頂點為B，O為坐標原點，|OA|=2|OB|．
  （1）若△BF₁F₂的面積為

  4

  3

  ，求橢圓C₁的標準方程；
  （2）如圖，過點P（1，0）作斜率k（k＞0）的直線l交橢圓C₁于不同兩點M，N，點M關于x軸對稱的點為S，直線SN交x軸于點T，點P在橢圓的內部，在橢圓上存在點Q，使

  OM

  +

  ON

  =

  OQ

  ，記四邊形OMQN的面積為S₁，求

  OT

  ?

  OQ

  -

  S

  2

  1

  k

  的最大值．
  組卷：169引用：4難度：0.3

  解析