當前位置：試卷中心 > 試卷詳情

2012-2013學年安徽工大附中高二（下）開學數(shù)學試卷（理科）

發(fā)布：2025/1/5 23:30:2

1．下列條件中，能判定直線l⊥平面α的有（　　）
A．l與平面α內的兩條直線垂直
B．l與平面α內的無數(shù)條直線垂直
C．l與平面α內的任意一條直線垂直
D．l與平面α內的某一條直線垂直
組卷：749引用：7難度：0.9
解析
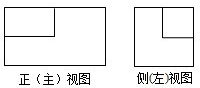2．一個長方體去掉一個小長方體，所得幾何體的正視圖與側（左）視圖分別如圖所，則該幾何體的俯視圖為（　　）
A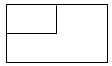． B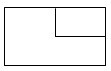． C． D．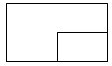
組卷：823引用：46難度：0.7
解析
3．已知命題p：“對?x∈R，?m∈R，使4^x+m?2^x+1=0”．若命題￢p是假命題，則實數(shù)m的取值范圍是（　　）
A．-2≤m≤2 B．m≥2 C．m≤-2 D．m≤-2或m≥2
組卷：53引用：5難度：0.9
解析
4．拋物線y=ax²的準線方程是y=2，則a的值為（　　）
A．
1
8
B．
-
1
8
C．8 D．-8
組卷：2082引用：80難度：0.9
解析
5．設F₁、F₂是橢圓
x
2
16
+
y
2
12
=
1
的兩個焦點，P是橢圓上的一點，且P到兩焦點的距離之差為2，則△PF₁F₂是（　　）
A．直角三角形 B．銳角三角形 C．斜三角形 D．鈍角三角形
組卷：468引用：9難度：0.7
解析
6．中心在原點，焦點在x軸上的雙曲線的一條漸近線經過點（4，-2），則它的離心率為（　　）
A．
6
B．
5
C．
6
2
D．
5
2
組卷：205引用：16難度：0.9
解析

19．已知圓C經過A（2，3），B（0，3）兩點，且與直線x+y-5=0相切，
（1）求圓C的標準方程；
（2）在直線x+y+1=0上任取一點P，過P點作圓C的切線，切點為Q，當|PQ|最小時，求切線PQ的斜率．
組卷：15引用：2難度：0.3
解析
20．已知拋物線C₁：x²+by=b²經過橢圓C₂：
x
2
a
2
+
y
2
b
2
=1（a＞b＞0）的兩個焦點．
（1）求橢圓C₂的離心率；
（2）設Q（3，b），又M，N為C₁與C₂不在y軸上的兩個交點，若△QMN的重心在拋物線C₁上，求C₁和C₂的方程．
組卷：684引用：6難度：0.1
解析

1．下列條件中，能判定直線l⊥平面α的有（ ）