2022-2023學年湖南省五市十校教研教改共同體高一（下）期中數學試卷

一、單選題

• 1．復數z=1+i的虛部是（　　）

  A．1

  B．-1

  C．i

  D．-i
  組卷：20引用：7難度：0.9

  解析

• 2．若正實數a、b滿足a+2b=1，則當ab取最大值時，a的值是（　　）

  A． 1 2

  B． 1 4

  C． 1 6

  D． 1 8
  組卷：684引用：5難度：0.7

  解析

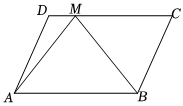• 3．如圖，在平行四邊形ABCD中，

  AB

  =

  a

  ，

  AD

  =

  b

  ，

  CM

  =

  4

  MD

  ，則

  AM

  =（　　）

  A． a + 1 5 b

  B． 1 5 a + b

  C． 1 5 a - b

  D． a - 1 5 b
  組卷：59引用：3難度：0.7

  解析

• 4．已知

  a

  =

  cos

  π

  3

  ，b=2^0.2，

  c

  =

  lo

  g

  2

  3

  ，則（　　）

  A．b＞c＞a

  B．b＞a＞c

  C．a＞c＞b

  D．a＞b＞c
  組卷：179引用：4難度：0.7

  解析

• 5．下列關于平面圖形的直觀圖的敘述中，正確的是（　　）

  A．等腰三角形的直觀圖仍是一個等腰三角形

  B．若某一平面圖形的直觀圖面積為a,則原圖形面積為 2 2 a

  C．原圖形中相等的線段，其直觀圖也一定相等

  D．若三角形的周長為12，則其直觀圖的周長為6
  組卷：34引用：3難度：0.7

  解析

• 6．函數f（x）=log₂x-sinx+

  1

  2

  的零點所在的區間為（　　）

  A．（ 1 4 ， 1 2 ）

  B．（ 1 2 ，1）

  C．（1，2）

  D．（2，3）
  組卷：89引用：2難度：0.6

  解析

• 7．若△ABC為銳角三角形，則（　　）

  A．sinA＞sinB	B．cosA＞cosB
  C．sin（cosA）＞sin（sinB）	D．cos（cosA）＞cos（sinB）
  組卷：78引用：3難度：0.6

  解析

四、解答題

• 21．對于函數f（x），g（x），若存在實數k使得函數h（x）=kf（x）?g（x），那么稱函數h（x）為f（x），g（x）的k積函數．
  （1）設函數f（x）=sinx,

  g

  （

  x

  ）

  =

  cos

  （

  x

  +

  2

  π

  3

  ）

  ，

  h

  （

  x

  ）

  =

  2

  sin

  （

  2

  x

  -

  π

  3

  ）

  +

  3

  ，試判斷h（x）是否為f（x），g（x）的k積函數？若是，請求出k的值；若不是，請說明理由；
  （2）設函數

  f

  （

  x

  ）

  =

  mx

  +

  n

  x

  （其中m＞0，n＞0，x＞0），且函數f（x）圖象的最低點坐標為（2，4），若函數g（x）=f（2-x），h（x）是f（x），g（x）的1積函數，且對于任意實數x∈（0，2），h（x）≥a恒成立，求實數a的取值范圍．
  組卷：32引用：3難度：0.5

  解析

• 22．在銳角△ABC中，角A，B，C所對的邊分別是a,b,c,已知b=2，

  a

  b

  =

  3

  3

  sinC+cosC．
  （1）求角B；
  （2）若M是△ABC內的一動點，且滿足

  BM

  =

  MA

  +

  MC

  ，則|

  BM

  |是否存在最大值？若存在，請求出最大值及取最大值的條件；若不存在，請說明理由；
  （3）若D是△ABC中AC上的一點，且滿足

  BA

  ?

  BD

  |

  BA

  |

  =

  BD

  ?

  BC

  |

  BC

  |

  ，求AD：DC的取值范圍．
  組卷：350引用：6難度：0.3

  解析