2020-2021學(xué)年重慶十八中九年級(下)入學(xué)數(shù)學(xué)試卷
發(fā)布:2024/4/20 14:35:0
一、單選題(每小題4分,共48分)
-
1.下列四個數(shù)中,是無理數(shù)的是( )
A.0 B. 203C. 4D. 17組卷:2引用:1難度:0.7 -
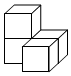 2.如圖是由4個相同的小正方體組成的幾何體,從上往下看到的平面圖形為( )
2.如圖是由4個相同的小正方體組成的幾何體,從上往下看到的平面圖形為( )A. 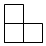
B. 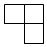
C. 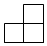
D. 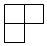 組卷:45引用:6難度:0.8
組卷:45引用:6難度:0.8 -
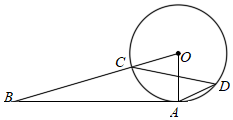 3.如圖,AB為⊙O的切線,點(diǎn)A為切點(diǎn),OB交⊙O于點(diǎn)C,點(diǎn)D在⊙O上,連接AD、CD,OA,若∠ABO=20°,則∠ADC的度數(shù)為( )
3.如圖,AB為⊙O的切線,點(diǎn)A為切點(diǎn),OB交⊙O于點(diǎn)C,點(diǎn)D在⊙O上,連接AD、CD,OA,若∠ABO=20°,則∠ADC的度數(shù)為( )A.20° B.30° C.35° D.40° 組卷:609引用:3難度:0.7 -
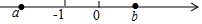 4.實(shí)數(shù)a,b在數(shù)軸上對應(yīng)點(diǎn)的位置如圖所示,且|a|>|b|,則化簡+|a+b|的結(jié)果為( )a2
4.實(shí)數(shù)a,b在數(shù)軸上對應(yīng)點(diǎn)的位置如圖所示,且|a|>|b|,則化簡+|a+b|的結(jié)果為( )a2A.2a+b B.-2a-b C.b D.2a-b 組卷:3129引用:13難度:0.8 -
5.將一半徑相同的小圓按如圖所示的規(guī)律擺放,第1個圖形有4個小圓,第2個圖形有8個小圓,第3個圖形有14個小圓,…,依此規(guī)律,第9個圖形的小圓個數(shù)是( )
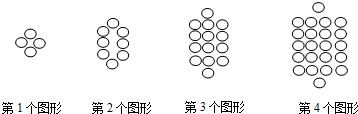
A.36 B.74 C.90 D.92 組卷:324引用:11難度:0.7 -
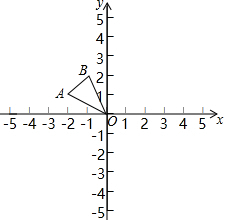 6.如圖,在平面直角坐標(biāo)系中,已知點(diǎn)A(-2,1),B(-1,2),以原點(diǎn)O為位似中心,相似比為2,把△ABO放大,則點(diǎn)B的對應(yīng)點(diǎn)B′的坐標(biāo)是( )
6.如圖,在平面直角坐標(biāo)系中,已知點(diǎn)A(-2,1),B(-1,2),以原點(diǎn)O為位似中心,相似比為2,把△ABO放大,則點(diǎn)B的對應(yīng)點(diǎn)B′的坐標(biāo)是( )A.(-4,2) B.(-2,4) C.(-4,2)或(-2,4) D.(-2,4)或(2,-4) 組卷:844引用:3難度:0.5 -
7.下列命題中,其逆命題是真命題的有( )個.
①全等三角形的對應(yīng)角相等;
②兩直線平行,同位角相等;
③等腰三角形的兩個底角相等;
④正方形的四個角相等.A.1 B.2 C.3 D.4 組卷:16引用:1難度:0.6 -
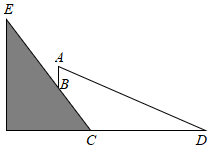 8.如圖,某建筑物AB在一個坡度為i=1:0.75的山坡CE上,建筑物底部點(diǎn)B到山腳點(diǎn)C的距離BC=20米,在距山腳點(diǎn)C右側(cè)水平距離為60米的點(diǎn)D處測得建筑物頂部點(diǎn)A的仰角是24°,建筑物AB和山坡CE的剖面的同一平面內(nèi),則建筑物AB的高度約為( )
8.如圖,某建筑物AB在一個坡度為i=1:0.75的山坡CE上,建筑物底部點(diǎn)B到山腳點(diǎn)C的距離BC=20米,在距山腳點(diǎn)C右側(cè)水平距離為60米的點(diǎn)D處測得建筑物頂部點(diǎn)A的仰角是24°,建筑物AB和山坡CE的剖面的同一平面內(nèi),則建筑物AB的高度約為( )
(參考數(shù)據(jù):sin24°≈0.41,cos24°≈0.91,tan24°≈0.45)A.32.4米 B.20.4米 C.16.4米 D.15.4米 組卷:171引用:6難度:0.5
三、解答題
-
25.如圖1,在平面直角坐標(biāo)系中,拋物線與x軸交于點(diǎn)A(-1,0),B(點(diǎn)A在點(diǎn)B的左側(cè)),交y軸于點(diǎn)(0,-3),拋物線的對稱軸為直線x=1,點(diǎn)D為拋物線的頂點(diǎn).
(1)求該拋物線的解析式;
(2)已知經(jīng)過點(diǎn)A的直線y=kx+b(k>0)與拋物線在第一象限交于點(diǎn)E,連接AD,DE,BE,當(dāng)S△ADE=2S△ABE時,求點(diǎn)E的坐標(biāo);
(3)如圖2,在(2)中直線AE與y軸交于點(diǎn)F,將點(diǎn)F向下平移+23個單位長度得到點(diǎn)Q,連接QB.將△OQB繞點(diǎn)O逆時針旋轉(zhuǎn)一定的角度α(0°<α<360°)得到△OQ′B′,直線B′Q′與x軸交于點(diǎn)G.問在旋轉(zhuǎn)過程中是否存在某個位置使得△OQ′G是等腰三角形?若存在,請直接寫出所有滿足條件的點(diǎn)Q′的坐標(biāo);若不存在,請說明理由.3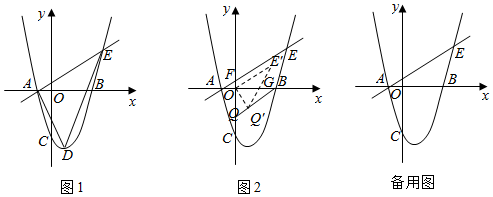 組卷:483引用:2難度:0.1
組卷:483引用:2難度:0.1 -
26.在△ABC中,∠ACB=90°,AC=BC,點(diǎn)D是直線AB上的一動點(diǎn)(不與點(diǎn)A,B重合)連接CD,在CD的右側(cè)以CD為斜邊作等腰直角三角形CDE,點(diǎn)H是BD的中點(diǎn),連接EH.
【問題發(fā)現(xiàn)】
(1)如圖(1),當(dāng)點(diǎn)D是AB的中點(diǎn)時,線段EH與AD的數(shù)量關(guān)系是 ,EH與AD的位置關(guān)系是 .
【猜想論證】
(2)如圖(2),當(dāng)點(diǎn)D在邊AB上且不是AB的中點(diǎn)時,(1)中的結(jié)論是否仍然成立?若成立,請僅就圖(2)中的情況給出證明;若不成立,請說明理由.
【拓展應(yīng)用】
(3)若AC=BC=2,其他條件不變,連接AE、BE.當(dāng)△BCE是等邊三角形時,請直接寫出△ADE的面積.2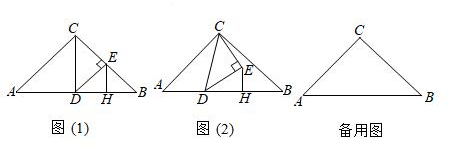 組卷:3414引用:18難度:0.1
組卷:3414引用:18難度:0.1


