2012-2013學年浙江省嘉興市桐鄉市實驗中學九年級（上）數學競賽模擬試卷（一）

一、選擇題（每題3分，共27分）

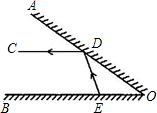• 1．如圖所示，∠AOB的兩邊．OA、OB均為平面反光鏡，∠AOB=35°，在OB上有一點E，從E點射出一束光線經OA上的點D反射后，反射光線DC恰好與OB平行，則∠DEB的度數是（　　）

  A．35°

  B．70°

  C．110°

  D．120°
  組卷：563引用：19難度：0.9

  解析

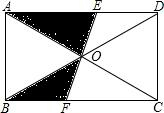• 2．如圖，矩形ABCD的對角線相交于點O，過O點的直線與AD、BC相交于點E，F，則圖中陰影部分的面積與矩形ABCD的面積之比是（　　）

  A．1：2

  B．1：3

  C．1：4

  D．2：5
  組卷：147引用：1難度：0.9

  解析

• 3．已知拋物線y=ax²+bx+c（a＜0）過A（-2，0）、B（0，0）、C（-3，y₁）、D（3，y₂）四點，則y₁與y₂的大小關系是（　　）

  A．y1＞y2

  B．y1=y2

  C．y1＜y2

  D．不能確定
  組卷：727引用：61難度：0.9

  解析

• 4．下列各式子的運算：①（3a²b²）²?2b³=18a⁴b⁶；②

  -

  1

  a

  =

  -

  a

  ；③a⁰=1；④

  a

  8

  =

  a

  6

  ；⑤

  （

  -

  7

  2

  7

  ）

  2

  =

  14

  ；⑥

  |

  4

  3

  -

  7

  |

  =

  7

  -

  4

  3

  ．其中計算正確的有（　　）

  A．1個

  B．2個

  C．3個

  D．4個
  組卷：174引用：1難度：0.9

  解析

• 5．若函數

  y

  =

  x 2 + 2 （ x ≤ 2 ）

  2 x （ x ＞ 2 ）

  ，則當函數值y=8時，自變量x的值是（　　）

  A．± 6

  B．4

  C．± 6 或4

  D．4或- 6
  組卷：14865引用：126難度：0.5

  解析

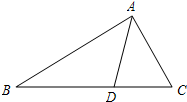• 6．已知：如圖，AD是△ABC的角平分線，且AB：AC=

  3

  ：

  2

  ，則△ABD與△ACD的面積之比為（　　）

  A．3：2

  B． 3 ： 2

  C．2：3

  D． 2 ： 3
  組卷：890引用：21難度：0.9

  解析

三、解答題（第15題6分，第16，17題各7分，第18題8分，共28分）

• 17．為了抓住梵凈山文化藝術節的商機，某商店決定購進A、B兩種藝術節紀念品．若購進A種紀念品8件，B種紀念品3件，需要950元；若購進A種紀念品5件，B種紀念品6件，需要800元．
  （1）求購進A、B兩種紀念品每件各需多少元？
  （2）若該商店決定購進這兩種紀念品共100件，考慮市場需求和資金周轉，用于購買這100件紀念品的資金不少于7500元，但不超過7650元，那么該商店共有幾種進貨方案？
  （3）若銷售每件A種紀念品可獲利潤20元，每件B種紀念品可獲利潤30元，在第（2）問的各種進貨方案中，哪一種方案獲利最大？最大利潤是多少元？
  組卷：9021引用：43難度：0.5

  解析

• 18．如圖，在平面直角坐標系中，點P從原點O出發，沿x軸向右以每秒1個單位長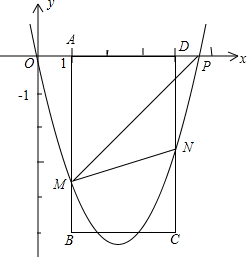的速度運動t秒（t＞0），拋物線y=x²+bx+c經過點O和點P，已知矩形ABCD的三個頂點為A（1，0），B（1，-5），D（4，0）．
  （1）求c,b（用含t的代數式表示）：
  （2）當4＜t＜5時，設拋物線分別與線段AB，CD交于點M，N．
  ①在點P的運動過程中，你認為∠AMP的大小是否會變化？若變化，說明理由；若不變，求出∠AMP的值；
  ②求△MPN的面積S與t的函數關系式，并求t為何值時，

  S

  =

  21

  8

  ；
  （3）在矩形ABCD的內部（不含邊界），把橫、縱坐標都是整數的點稱為“好點”．若拋物線將這些“好點”分成數量相等的兩部分，請直接寫出t的取值范圍．
  組卷：1491引用：17難度：0.5

  解析