當前位置：試卷中心 > 試卷詳情

2023-2024學年安徽省高一（上）期中數學試卷

發布：2024/10/12 1:0:1

一、選擇題：本題共8小題，每小題5分，共40分。在每小題給出的四個選項中，只有一項是符合題目要求的。

1．已知集合M={-1，0，1}，集合N={x∈R|x²=2x}，則M∩N=（　　）
A．{0，1} B．{-1，0} C．{0} D．?
組卷：21引用：2難度：0.7
解析
2．已知命題p：?x∈R，4^x＞x⁴，則?p是（　　）
A．?x∈R，4^x≤x⁴ B．?x∈R，4^x＜x⁴ C．?x∈R，4^x＞x⁴ D．?x∈R，4^x≤x⁴
組卷：9引用：2難度：0.8
解析
3．若α是β的必要不充分條件，γ是β的充要條件，則γ是α的（　　）
A．充分不必要條件 B．必要不充分條件
C．充分必要條件 D．既不充分也不必要條件
組卷：10引用：1難度：0.7
解析
4．已知冪函數f（x）=x^α（α∈Z），具有如下性質：f²（1）+f²（-1）=2[f（1）+f（-1）-1]，則f（x）是（　　）
A．奇函數 B．偶函數
C．既是奇函數又是偶函數 D．是非奇非偶函數
組卷：145引用：6難度：0.9
解析
5．函數
f
（
x
）
=
x
+
3
，
x
≤
0
x
，
x
＞
0
，且f（a-3）=f（a+2）（a∈R），則f（a）=（　　）
A．2 B．1 C．
2
D．0
組卷：5引用：1難度：0.8
解析
6．已知實數a,b,c滿足3×2^a-2^b+1=0，且a=c+x²-x+1（x∈R），則a,b,c的大小關系是（　　）
A．a＞b＞c B．b＞a＞c C．a＞c＞b D．c＞b＞a
組卷：22引用：1難度：0.7
解析
7．水池有兩個相同的進水口和一個出水口，每個口進出的速度如圖甲乙所示．某天零點到六點該水池的蓄水量如圖丙所示（至少打開一個水口）．給出以下三個論斷：①零點到三點只進水不出水；②三點到四點不進水只出水；③四點到六點不進水也不出水．其中正確論斷的序號是（　　）
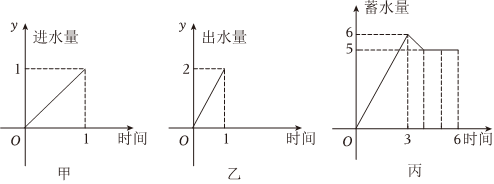
A．①② B．②③ C．①③ D．①
組卷：4引用：1難度：0.5
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題：共70分。解答應寫出文字說明、證明過程或演算步驟。

21．我們知道，
（
a
+
b
2
）
2
≤
a
2
+
b
2
2
，當且僅當a=b時等號成立．即a,b的算術平均數的平方不大于a,b平方的算術平均數．此結論可以推廣到三元，即
（
a
+
b
+
c
3
）
2
≤
a
2
+
b
2
+
c
2
3
，當且僅當a=b=c時等號成立．
（1）證明：
（
a
+
b
+
c
3
）
2
≤
a
2
+
b
2
+
c
2
3
，當且僅當a=b=c時等號成立．
（2）已知x＞0，y＞0，z＞0，若不等式
x
+
y
+
z
≤
t
x
+
y
+
z
恒成立，利用（1）中的不等式，求實數t的最小值．
組卷：18引用：2難度：0.4
解析
22．已知函數
f
（
x
）
=
x
，
（
0
≤
x
＜
n
）
（
x
-
1
）
2
，
（
x
≥
n
）
，其中n＞1．若存在實數b,使得關于x的方程f（x）=b有兩個不同的實數根．
（1）求n的整數值；
（2）設函數g（x）=x²+a|x-n|，n取（1）中的整數值．若g（x）在[0，+∞）上單調遞增，求實數a的取值范圍．
組卷：14引用：1難度：0.6
解析