2022-2023學年江西省宜春市豐城中學高三（上）第四次段考數學試卷（理科）

一、選擇題（本題包括12小題，每小題5分，共60分。在每小題給出的四個選項中只有一項是符合題目要求的）

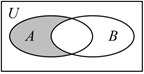• 1．下邊的Venn圖中，兩個橢圓區域對應集合A，B，其中A={-2，-1，0，1，2}，B={x∈N|x＜5}．則陰影部分表示（　　）

  A．{0，1，2}

  B．{3，4}

  C．{-2，-1}

  D．{-2，-1，0}
  組卷：51引用：4難度：0.7

  解析

• 2．下列條件是“過點（a,2）可以作兩條與曲線y=2^x-1相切的直線”的充分條件的是（　　）

  A．a＜1

  B．a＜2

  C．a＞e

  D．a＞ln2
  組卷：25引用：4難度：0.6

  解析

• 3．使3^|x-3|+（x-3）sin（x-3）+kcos（x-3）=0有唯一的解的k有（　　）

  A．不存在

  B．1個

  C．2個

  D．無窮多個
  組卷：164引用：3難度：0.4

  解析

• 4．如圖，由于建筑物AB的底部B是不可能到達的，A為建筑物的最高點，需要測量AB，先采取如下方法，選擇一條水平基線HG，使得H，G，B三點在一條直線上，在G，H兩點用測角儀測得A的仰角為α，β，CD=a,測角儀器的高度是h,則建筑物AB的高度為（　　）

  A． asinβ sin （ α - β ） + h	B． asinα sin （ α - β ） + h
  C． asinαsinβ sin （ α - β ） + h	D． asinαsinβ cos （ α - β ） + h
  組卷：102引用：4難度：0.6

  解析

• 5．記△ABC所在平面內一點為P，滿足

  x

  AB

  +

  y

  AC

  =

  AP

  ，其中x²+y²=1，則

  S

  △

  ABP

  S

  △

  ABC

  的取值范圍為（　　）

  A． [ 2 - 1 ， + ∞ ）

  B． （ 0 ， 2 - 1 ]

  C．（0，1]

  D． [ 2 + 1 ， + ∞ ）
  組卷：2引用：2難度：0.6

  解析

• 6．已知函數f₀（x）=e^xx,記函數f_n（x）為f_（n-1）（x）的導函數（n∈N^*），函數y=f_n（x）的圖象在x=1處的切線與x軸相交的橫坐標為x_n，則

  n

  ∑

  i

  =

  1

  x

  i

  x

  i

  +

  1

  =（　　）

  A． n + 1 3 （ n + 2 ）	B． n 3 （ n + 3 ）
  C． n （ n + 2 ） （ n + 3 ）	D． n + 1 （ n + 2 ） （ n + 3 ）
  組卷：106引用：4難度：0.5

  解析

• 7．下列各式大小比較中，其中正確的是（　　）

  A． 7 - 5 ＞ 5 - 3	B． tan 4 ＜ sin （ - 19 π 15 ）
  C．2ln3＜3ln2	D． log 1 5 1 2 ＜ （ 1 2 ） 1 5
  組卷：8引用：1難度：0.6

  解析

三、解答題（本大題共6小題，共70分。解答應寫出必要的文字說明、證明過程或演算步驟）

• 21．設A，B，C是△ABC的三個內角，△ABC的面積S滿足1≤S≤

  3

  ，且

  CA

  ?

  CB

  =2，∠ACB=θ．
  （1）若向量

  m

  =（sin2A，cos2A），

  n

  =（cos2B，sin2B），求

  |

  2

  m

  -

  3

  n

  |的取值范圍；
  （2）求函數

  f

  （

  θ

  ）

  =

  sin

  （

  θ

  -

  π

  4

  ）

  +

  4

  2

  sinθcosθ

  -

  cos

  （

  θ

  +

  π

  4

  ）

  的最大值．
  組卷：8引用：2難度：0.4

  解析

• 22．設函數f（x）=xlna-alnx,a＞1．
  （1）若對任意x∈[4，+∞），都有f（x）≥0，求a的取值范圍；
  （2）設g（x,n）=f（x）+f（x²）+…+f（xⁿ），n∈N^*．當0＜x＜1時，判斷g（x,n），g（x,2n），g（x,3n）是否能構成等差數列，并說明理由．
  組卷：54引用：2難度：0.3

  解析