2022-2023學年天津市和平區高三（上）期末數學試卷

一、選擇題（在每小題給出的四個選項中，只有一項是符合題目要求的）

• 1．設全集U={-2，-1，0，1，2，3}，集合A={-1，2}，B={x|x²-4x+3=0}，則?_U（A∪B）=（　　）

  A．{1，3}

  B．{0，3}

  C．{-2，0}

  D．{-2，1}
  組卷：759引用：14難度：0.7

  解析

• 2．“n是3的倍數”是“n是6的倍數”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充要條件	D．既不充分又不必要條件
  組卷：168引用：1難度：0.8

  解析

• 3．函數f（x）=

  2

  ln

  |

  x

  |

  x

  的部分圖象大致為（　　）

  A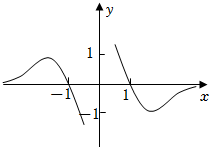．	B．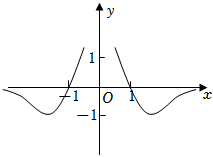
  C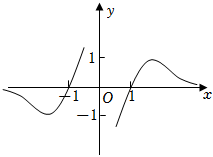．	D．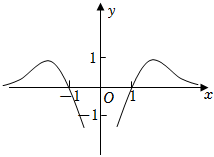
  組卷：577引用：10難度：0.7

  解析

• 4．若棱長為

  3

  的正方體的頂點都在同一球面上，則該球的體積為（　　）

  A． 9 2 π

  B． 27 8 π

  C．9π

  D．27π
  組卷：449引用：2難度：0.6

  解析

• 5．為倡導“節能減排，低碳生活”的理念，某社區對家庭的人均月用電量情況進行了調查，通過抽樣，獲得了某社區100個家庭的人均月用電量（單位：千瓦時），將數據按照[40，60），[60，80），[80，100），[100，120），[120，140），[140，160]分成6組，制成了如圖所示的頻率分布直方圖．若該社區有3000個家庭，估計全社區人均月用電量低于80千瓦時的家庭數為（　　）

  A．300

  B．450

  C．480

  D．600
  組卷：333引用：3難度：0.8

  解析

• 6．設a=log_0.62，b=log₂0.6，c=0.6²，則a,b,c的大小關系為（　　）

  A．b＜c＜a

  B．c＜b＜a

  C．a＜b＜c

  D．b＜a＜c
  組卷：529引用：4難度：0.7

  解析

三、解答題（本大題共5小題，共75分，解答應寫出文字說明，證明過程或演算步驟）

• 19．已知數列{a_n}是公差為1的等差數列，且a₁+a₂=a₃，數列{b_n}是等比數列，且b₁?b₂=b₃，a₄=4b₁-b₂．
  （Ⅰ）求{a_n}和{b_n}的通項公式；
  （Ⅱ）設

  c

  n

  =

  a

  n

  +

  1

  b

  2

  n

  ，（n∈N^*），求數列{c_n}的前n項和S_n；
  （Ⅲ）設

  d

  n

  =

  15 a n + 32 4 a n a n + 2 b 2 n ， n 為奇數 ，

  a n + b n ， n 為偶數 .

  （

  n

  ∈

  N

  *

  ）

  ，求數列{d_n}的前2n項和T_2n．
  組卷：461引用：4難度：0.3

  解析

• 20．已知函數f（x）=lnx,g（x）=x²-x+1，h（x）=f（x）-g（x）．
  （Ⅰ）求函數h（x）的極值；
  （Ⅱ）證明：有且只有兩條直線與函數f（x），g（x）的圖象都相切；
  （Ⅲ）若2ae^2x+lna≥f（x）恒成立，求實數a的最小值．
  組卷：334引用：5難度：0.2

  解析